Phương pháp tính khoảng cách từ một điểm đến một mặt phẳng

Bài toán: Bạn có một điểm A có tọa độ (x₀, y₀, z₀) và một mặt phẳng được định bởi phương trình ax + by + cz + d = 0. Bạn muốn tính khoảng cách từ điểm A đến mặt phẳng.

Bước 1: Xác định các hệ số của mặt phẳng.

Mặt phẳng được biểu diễn bởi phương trình ax + by + cz + d = 0. Trong trường hợp này, bạn cần xác định các hệ số a, b, c và d.

Bước 2: Tính khoảng cách.

Để tính khoảng cách từ điểm A đến mặt phẳng, bạn có thể sử dụng công thức sau:

Khoảng cách = |(ax₀ + by₀ + cz₀ + d)| / √(a^2 + b^2 + c^2)

Trong đó:

• (x₀, y₀, z₀) là tọa độ của điểm A.
• a, b, c và d là các hệ số của mặt phẳng.

Ví dụ: Hãy tính khoảng cách từ điểm A(2, 3, 1) đến mặt phẳng 2x + 3y – z – 4 = 0.

Bước 1: Xác định các hệ số của mặt phẳng: a = 2, b = 3, c = -1, và d = -4.

Bước 2: Sử dụng công thức khoảng cách:

Khoảng cách = |(22 + 33 – 1*1 – 4)| / √(2^2 + 3^2 + (-1)^2) Khoảng cách = |(4 + 9 – 1 – 4)| / √(4 + 9 + 1) Khoảng cách = |8| / √14 Khoảng cách ≈ 8 / 3.74 ≈ 2.14 (đơn vị)

Vậy, khoảng cách từ điểm A đến mặt phẳng 2x + 3y – z – 4 = 0 là khoảng cách khoảng 2.14 đơn vị.

Ra mắt đến những em học viên lớp 12 bài viết Phương pháp tính khoảng cách từ một điểm đến một mặt phẳng, nhằm mục đích giúp những em học tốt chương trình Toán 12 .

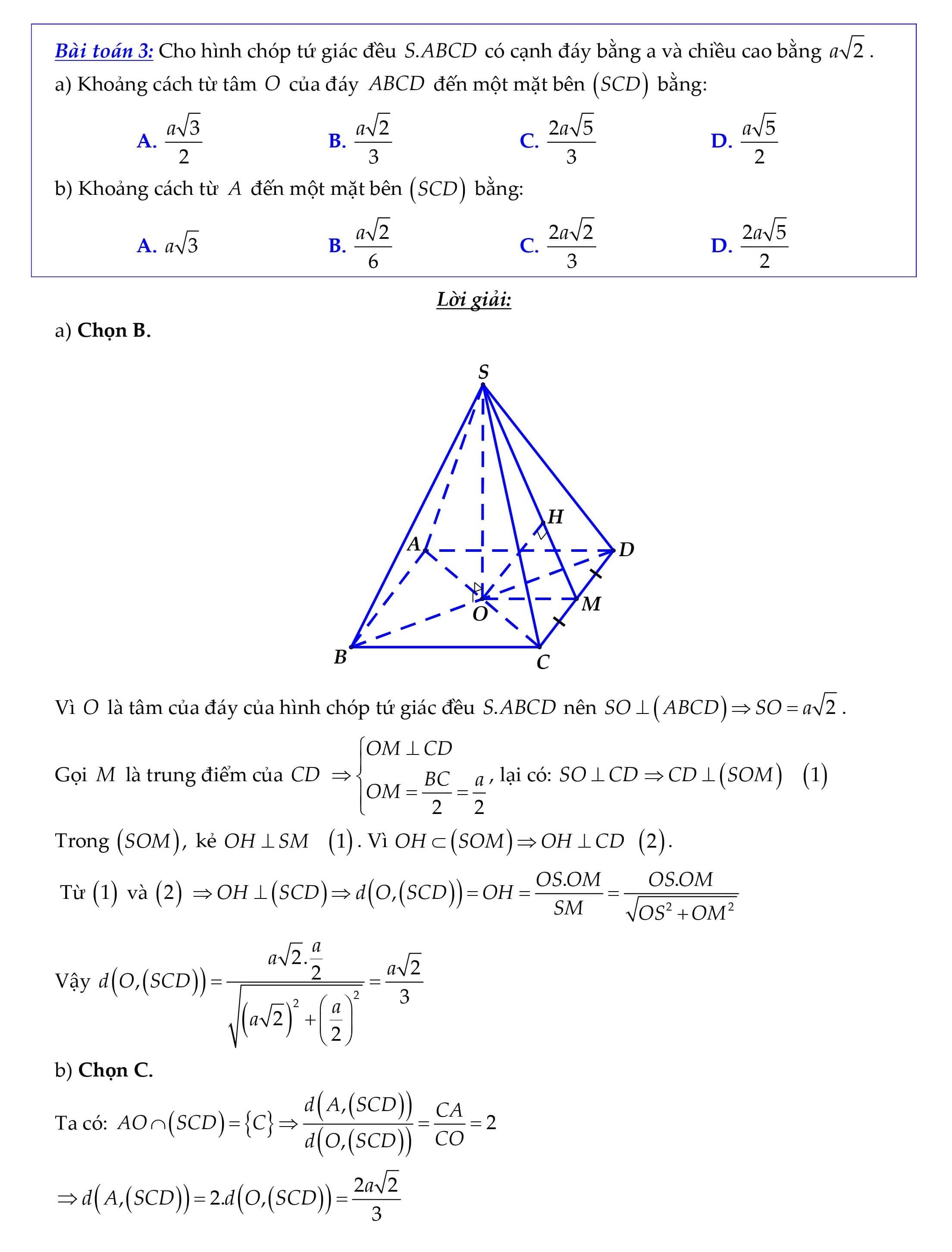
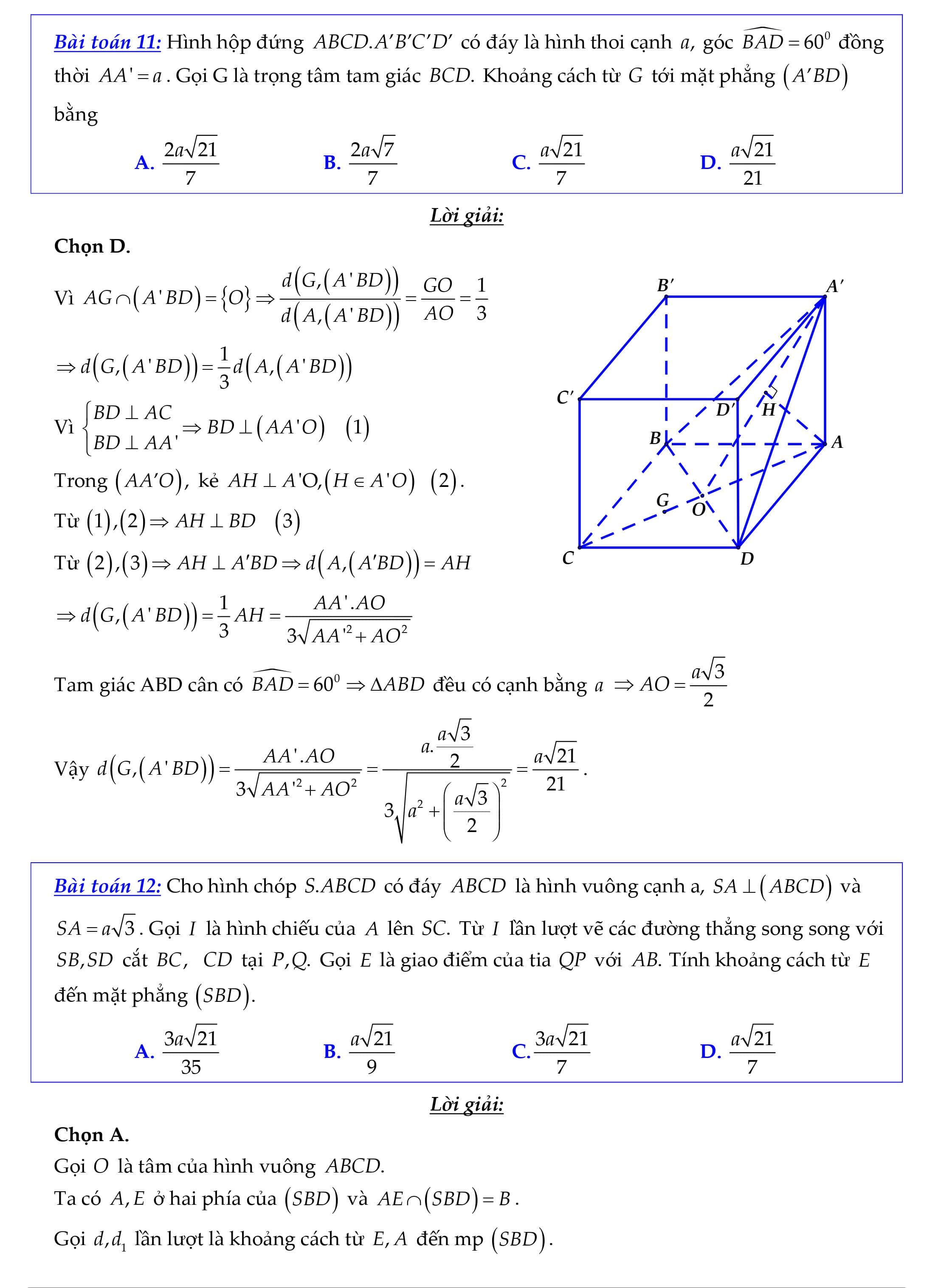
Nội dung bài viết Phương pháp tính khoảng cách từ một điểm đến một mặt phẳng:
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG Nhắc lại: Khoảng cách từ điểm M đến mặt phẳng (d) là MH, với H là hình chiếu của M trên mặt phẳng (d). Kí hiệu: PHƯƠNG PHÁP Bài toán: Tìm khoảng cách từ điểm 0 đến mặt phẳng (a). Như vậy, muốn tìm khoảng cách từ một điểm đến một mặt phẳng, trước hết ta phải tìm hình chiếu vuông góc của điểm đó trên mặt phẳng. Việc xác định hình chiếu của điểm trên mặt phẳng ta thường dùng một trong các cách sau: Cách 1: Bước 1. Tìm hình chiếu H của 0 lên (a). Tìm mặt phẳng (8) qua 0 oà vuông góc với (a). Tìm A = (a) (B). Trong mặt phẳng (8), kẻ OH IA tại H. PH là hình chiếu vuông góc của O lên (a). Bước 2. Khi đó OH là khoảng cách từ 0 đến (a). Lưu ý: Chọn mặt phẳng (8) sao cho dễ tìm giao tuyến với (a). Cách 2: Nếu đã có trước đường thẳng d (a) thì kẻ Ox cắt (a) tại H. Lúc đó, H là hình chiếu Ouông góc của.
Một số chú ý và thủ thuật giải khoảng cách quan trọng: Chú ý đến việc đưa bài toán tìm khoảng cách từ một điểm (đề bài cho bất kỳ đến một mặt phẳng về bài toán tìm khoảng cách từ chân đường cao đến mặt phẳng đó và tìm mối liên hệ giữa hai khoảng cách này. Từ đó suy ra được khoảng cách theo yêu cầu của đề bài. Khối chóp có các cạnh bên bằng nhau: Cho hình chóp có đỉnh S có các cạnh bên có độ dài bằng nhau: SA = SB = SC = SD. Khi đó hình chiếu 0 của S lên mặt phẳng đáy trùng với tâm đường tròn nội tiếp đi qua các đỉnh ( A, B, C, D,…) nằm trên mặt đáy. Nếu đáy là: Tam giác đều, O là trọng tâm. Tam giác vuông, O là trung điểm cạnh huyền. Hình vuông, hình chữ nhật, O là giao điểm của 2 đường chéo đồng thời là trung điểm mỗi đường. Sử dụng phương pháp thể tích để tìm khoảng cách: Đưa bài toán khoảng cách về bài toán tìm chiều cao của khối đa diện mà khối đa diện đó có thể xác định được dễ dàng thể tích và diện tích đáy. Phương pháp này được sử dụng trong trường hợp không thể tính được khoảng cách bằng cách công cụ tính toán như: định lí Pytago, các hệ thức lượng trong tam giác vuông, định lý cô-sin.
Các bài toán tính khoảng cách từ 1 điểm đến mặt phẳng hay gặp. Khoảng cách từ chân đường cao tới mặt bên. Bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách từ điểm H đến mặt bên (SAB). Khoảng cách từ một điểm trên mặt đáy tới mặt đứng (chứa đường cao). Bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách từ điểm A bất kì đến mặt bên (SHB).

Source: https://laodongdongnai.vn
Category: Điểm Đến