Đề số 8 – Đề kiểm tra học kì 2 – Toán 9 – https://laodongdongnai.vn

Bài 1.  Cho hai biểu thức \(A = \dfrac{{x + 12}}{{\sqrt x  – 1}}\) và \(B = \left( {\dfrac{3}{{x – 1}} + \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{1}{{\sqrt x  + 1}}\) với \(x \ge 0,x \ne 1\)

a ) Tính giá trị của biểu thức A khi x = 9b ) Rút gọn biểu thức B

c) Tìm giá trị nhỏ nhất của biểu thức \(M = \dfrac{A}{B}\)

Bài 2.  Giải bài toán bằng cách lập phương trình

Một công nhân dự định làm 33 sản phẩm trong thời hạn đã định. Nhưng thực tiễn nhà máy sản xuất lại giao 62 sản phẩm. Do vậy mặc dầu người đó đã làm tăng mỗi giờ 3 sản phẩm tuy nhiên vẫn hoàn thành xong chậm hơn dự định 1 giờ 30 phút. Tính năng suất dự định .

Bài 3.

1 ) Giải hệ phương trình : \ ( \ left \ { \ begin { array } { l } 3 \ sqrt { x – 3 } – \ dfrac { 1 } { { y + 1 } } = 1 \ \ \ sqrt { x – 3 } + \ dfrac { 2 } { { y + 1 } } = 5 \ end { array } \ right. \ )2 ) Cho Parabol \ ( y = { x ^ 2 } \ ) ( P ) và đường thẳng \ ( y = mx – m + 1 \ ) ( d ) .a ) Tìm tọa độ giao điểm của ( P ) và ( d ) với m = – 3 .b ) Tìm m để đường thẳng ( d ) và parabol ( P ) cắt nhau tại hai điểm phân biệt có hoành độ \ ( { x_1 }, { x_2 } \ ) thỏa mãn nhu cầu \ ( x_1 ^ 2 + x_2 ^ 2 = { x_1 } + { x_2 } \ ) .

Bài 4. Cho đường tròn (O; R), đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K khác A, hai dây MN và BK cắt nhau ở E.

a ) Chứng minh rằng AHEK là tứ giác nội tiếp .b ) Chứng minh CA. CK = CE. CHc ) Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. Chứng minh \ ( \ Delta NFK \ ) cân .d ) Giả sử KE = KC. Chứng minh OK / / MN

Bài 5.  Cho a, b, c là độ dài 3 cạnh của một tam giác biết:

a + b – c > 0 ; b + c – a > 0 ; c + a – b > 0Chứng minh : \ ( \ dfrac { 1 } { { a + b – c } } + \ dfrac { 1 } { { b + c – a } } + \ dfrac { 1 } { { c + a – b } } \ ) \ ( \, \ ge \ dfrac { 1 } { a } + \ dfrac { 1 } { b } + \ dfrac { 1 } { c } \ )\ ( \ Leftrightarrow { \ left ( { { x_1 } + { x_2 } } \ right ) ^ 2 } – 2 { x_1 } { x_2 } – \ left ( { { x_1 } + { x_2 } } \ right ) = 0 \ )\ ( \ Leftrightarrow { m ^ 2 } – 2 ( m – 1 ) – m = 0 \ )\ ( \ Leftrightarrow { m ^ 2 } – 3 m + 2 = 0 \ )\ ( \ Leftrightarrow \ left [ \ begin { array } { l } m = 1 ( TM ) \ \ m = 2 ( L ) \ end { array } \ right. \ )

Bài 4:

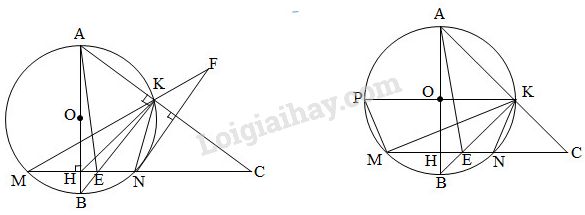
a ) Ta có : \ ( \ widehat { AHE } = { 90 ^ 0 } \ ) ( theo giả thiết \ ( AB \ bot MN ) \ )\ ( \ widehat { AKE } = { 90 ^ 0 } \ ) ( góc nội tiếp chắn nửa đường tròn )

\( \Rightarrow \widehat {AHE} + \widehat {AKE} = {180^0}\). Vậy tứ giác AHEK là tứ giác nội tiếp. (Tổng hai góc đối bằng 1800)

b ) Xét hai tam giác CAE và CHK :+ Có góc C chung+ \ ( \ widehat { EAC } = \ widehat { EHK } \ ) ( góc nội tiếp cùng chắn cùng EK )Suy ra ∆ CAE ~ ∆ CHA ( g – g )Suy ra CA. CK = CE. CHHoặc cm ∆ CKE ~ ∆ CHA ( g – g )c ) Do đường kính AB vuông góc MN nên B là điểm chính giữa cung MNSuy ra \ ( \ widehat { MKB } = \ widehat { NKB } \ ) ( 1 )Lại có BK / / NF ( vì cùng vuông góc với AC ) nên \ ( \ left \ { \ begin { array } { l } \ widehat { NKB } = \ widehat { KNF } ( 2 ) \ \ \ widehat { MKB } = \ widehat { MFN } ( 3 ) \ end { array } \ right. \ )Từ ( 1 ), ( 2 ), ( 3 ) suy ra \ ( \ widehat { MFN } = \ widehat { KNF } \ Leftrightarrow \ widehat { KFN } = \ widehat { KNF } \ ). Vậy \ ( \ Delta KNF \ ) cân tại K .d ) Ta có \ ( \ widehat { AKB } = { 90 ^ 0 } \ Rightarrow \ widehat { BKC } = { 90 ^ 0 } \ )\ ( \ Rightarrow \ Delta KEC \ ) vuông tại K .Theo giả thiết ta lại có KE = KC nên tam giác KEC vuông cân tại K\ ( \ widehat { BEH } = \ widehat { KEC } = { 45 ^ 0 } \ Rightarrow \ widehat { OBK } = { 45 ^ 0 } \ )Mặt khác vì tam giác OBK cân tại O ( do OB = OK = R ) nên suy ra tam giác OBK vuông cân tại O dẫn đến OK / / MN ( cùng vuông góc với AB )

Bài 5. 

Áp dụng bất đẳng thức CôsiVới x > 0, y > 0 ta có \ ( x + y \ ge 2 \ sqrt { xy } \ )\ ( { ( x + y ) ^ 2 } \ ge 4 xy \ Leftrightarrow \ dfrac { { x + y } } { { xy } } \ ge \ dfrac { 4 } { { x + y } } \ )\ ( \ dfrac { 1 } { x } + \ dfrac { 1 } { y } \ ge \ dfrac { 4 } { { x + y } } ( * ) \ )Dấu “ = ” xảy ra \ ( \ Leftrightarrow x = y \ )Áp dụng BĐT ( * ) ta có :\ ( \ dfrac { 1 } { { a + b – c } } + \ dfrac { 1 } { { b + c – a } } \ ) \ ( \, \ ge \ dfrac { 4 } { { a + b – c + b + c – a } } = \ dfrac { 4 } { { 2 b } } \ ) \ ( \, = \ dfrac { 2 } { b } ( 1 ) \ )

Tương tự: \(\dfrac{1}{{c + a – b}} + \dfrac{1}{{b + c – a}} \ge \dfrac{2}{c}(2)\)

\ ( \ dfrac { 1 } { { c + a – b } } + \ dfrac { 1 } { { a + b – c } } \ ge \ dfrac { 2 } { a } ( 3 ) \ )Cộng ( 1 ), ( 2 ), ( 3 ) vế với vế ta có :\ ( \ dfrac { 1 } { { a + b – c } } + \ dfrac { 1 } { { b + c – a } } + \ dfrac { 1 } { { c + a – b } } \ ) \ ( \, \ ge \ dfrac { 1 } { a } + \ dfrac { 1 } { b } + \ dfrac { 1 } { c } \ ). Dấu “ = ” xảy ra \ ( \ Leftrightarrow a = b = c \ )

Source: https://laodongdongnai.vn
Category: Người Lao Động