Tổng hợp lý thuyết vecto lớp 10 đầy đủ và chi tiết nhất – TÀI LIỆU RẺ
Vecto lớp 10 là chương đầu tiên của hình học THPT. Bài viết này sẽ giúp các em hiểu một cách hoàn toàn về định nghĩa, tính chất, cách ứng dụng vecto vào toán học sau này trước khi tìm hiểu qua các dạng bài tập mà tailieure.com trình bày. Vecto lớp 10 được cho là phần kiến thức nền tảng nhất cho hình học 10 vì thế trước khi nắm kĩ các dạng bài tập ở dưới, các em cần phải nắm thật kĩ lý thuyết. Hãy cùng tìm hiểu các vấn đề lý thuyết dưới đây ^ ^
TẢI XUỐNG PDF ↓
Định nghĩa cơ bản về vecto lớp 10:
Định nghĩa vecto lớp 10
Trong toán học sơ cấp, véc-tơ là một đoạn thẳng có hướng. Ví dụ trong mặt phẳng cho hai điểm phân biệt A và B bất kì ta có thể xác định được véctơ.
Trong chương trình lớp 10, người ta định nghĩa:
- Vectơ là một đoạn thẳng định hướng.
- Vectơ có điểm đầu là \[A\], điểm cuối \[B\] là vectơ \[AB\], kí hiệu \[\overrightarrow{AB}\]. Khi không cần chỉ rõ điểm đầu, điểm cuối vectơ còn được kí hiệu \[\vec{a},\vec{b}\]…
- Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ.
Vec tơ cùng phương, vectơ cùng hướng.
- – Hai vec tơ cùng phương nếu giá của chúng song song hoặc trùng nhau.
- – Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng nếu chúng cùng phương.
Hai vectơ bằng nhau.
Độ dài của vecto: Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó hay nói gọn hơn, độ dài của vectơ \[\overrightarrow{AB}\] là độ dài đoạn thẳng \[AB\], kí hiệu \[\left| \overrightarrow{AB} \right|\].
Tính chất: \[\left| \overrightarrow{AB} \right|=AB\]
- Độ dài vectơ là một số không âm.
- Vec tơ có độ dài bằng \[1\] gọi là vectơ đơn vị.
- Hai vectơ bằng nhau nếu chúng cùng hướng và có cùng độ dài.
- \[\overrightarrow{AB}=\overrightarrow{CD}\Leftrightarrow \overrightarrow{AB}\] cùng hướng với \[\overrightarrow{CD}\] và \[\left| \overrightarrow{AB} \right|=\left| \overrightarrow{CD} \right|\]
- Khi cho trước một vectơ \[{\vec{a}}\] và một vectơ \[0\] trong mặt phẳng, ta luôn tìm được một điểm \[A\] để có \[\overrightarrow{OA}=\vec{a}\].
- Điểm \[A\] như vậy là duy nhất.
Vec tơ- không.
Vectơ- không kí hiệu là \[{\vec{0}}\] là vectơ có điểm đầu và điểm cuối trùng nhau:
\[\overrightarrow{AA}=\overrightarrow{BB}=\vec{0}\]
Vectơ- không có độ dài bằng \[0\] và hướng tùy ý
Tổng hiệu của hai vecto ( vecto lớp 10)
Tổng của hai vectơ
Định nghĩa: Cho hai vectơ \[\vec{a},\vec{b}\]. Lấy một điểm \[A\] tùy ý, vẽ \[\overrightarrow{AB}=a\], \[\overrightarrow{BC}=\vec{b}\]. Vectơ \[\overrightarrow{AC}\] được gọi là tổng của hai vectơ \[{\vec{a}}\] và \[{\vec{b}}\].
\[\overrightarrow{AC}=\vec{a}+\vec{b}\].
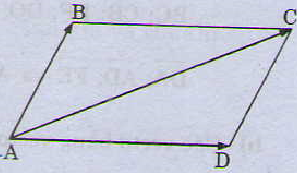
Quy tắc hình bình hành
Nếu \[ABCD\] là hình bình hành thì
\[\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\].
Tính chất của tổng các vectơ:
– Tính chất giao hoán \[\vec{a}+\vec{b}=\vec{b}+\vec{a}\].
– Tính chất kết hợp \[(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\].
– Tính chất của \[\vec{0};\vec{a}+\vec{0}=\vec{0}+\vec{a}\].
Hiệu của hai vectơ:
Vec tơ đối:
Vectơ có cùng độ dài và ngược hướng với vec tơ \[{\vec{a}}\] được gọi là vec tơ đối của vec tơ \[{\vec{a}}\], kí hiệu \[-\vec{a}\].
Vec tơ đối của \[{\vec{0}}\] là vectơ \[{\vec{0}}\].
Hiệu của hai vec tơ:
Cho hai vectơ \[\vec{a},\vec{b}\]. Vec tơ hiệu của hai vectơ, kí hiệu \[\vec{a}-\vec{b}\] là vectơ \[\vec{a}+(-\vec{b})\].
\[\vec{a}-\vec{b}=\vec{a}+(-\vec{b})\].
Chú ý:
Với ba điểm bất kì, ta luôn có
\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\] (1)
\[\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}\] (2)
(1) là quy tắc 3 điểm (quy tắc tam giác) đối với tổng của hai vectơ.
(2) là quy tắc 3 điểm (quy tắc tam giác) đối với hiệu các vectơ.
Áp dụng:
Trung điểm của đoạn thẳng:
\[I\] là trung điểm của đoạn thẳng \[\Leftrightarrow \] \[\overrightarrow{IA}+\overrightarrow{IB}=\vec{0}\].
Trọng tâm của tam giác:
\[G\] là trọng tâm của tam giác ∆ABC \[\Leftrightarrow \] \[\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\].
Lý thuyết hệ trục tọa độ: (vecto lớp 10)
Trục và độ dài đại số trên trục:
Trục tọa độ:
Trục tọa độ là một đường thẳng trên đó đã xác định một điểm gốc \[O\] và một vec tơ đơn vị \[\overrightarrow{e}\]
![]()
Tọa độ của một điểm:
Ứng với mỗi điểm \[M\] trên trục tọa độ thì có một số thực \[k\] sao cho
\[\overrightarrow{OM}=k\vec{e}\]
Số \[k\] được gọi là tọa độ của điểm \[M\] đối với trục đã cho.
Độ dài đại số:
Cho hai điểm \[A,B\] trên trục số, tồn tại duy nhất một số \[a\] sao cho \[\overrightarrow{AB}=a\vec{e}\]
\[a\] được gọi là độ dài đại số của vectơ \[\overrightarrow{AB}\], kí hiệu \[a=\overrightarrow{AB}\].
Chú ý:
– Nếu vectơ \[\overrightarrow{AB}\] cùng hướng với vec tơ đơn vị \[{\vec{e}}\] của trục thì\[\overline{AB}>0\], còn nếu \[\overrightarrow{AB}\] ngược hướng với vec tơ đơn vị \[{\vec{e}}\] thì \[\overline{AB}<0\]
– Nếu điểm \[A\] có tọa độ trên trục là \[a\] và điểm \[B\] có tọa độ là \[b\] thì
\[\overline{AB}=b-a\]
Hệ trục tọa độ:
Định nghĩa:
Hệ trục tọa độ \[\left( 0;\vec{i};\vec{j} \right)\] gồm hai trục \[\left( 0;\vec{i} \right)\] và \[\left( 0;\vec{j} \right)\] vuông góc với nhau.
\[O\] là gốc tọa độ
\[\left( 0;\vec{i} \right)\] là trục hoành
\[\left( 0;\vec{j} \right)\] là trục tung
\[\left| \overrightarrow{i} \right|=\left| \overrightarrow{j} \right|=1\]
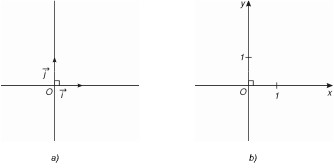
Mặt phẳng được trang bị một hệ tọa độ được gọi là mặt phẳng tọa độ.
Tọa độ vectơ
\[\overrightarrow{u}=x\vec{i}+y\vec{j}\Leftrightarrow u(x;y)\]
Hai vectơ bằng nhau khi và chỉ khi các tọa độ tương ứng bằng nhau
\[\overrightarrow{u}(x;y);\overrightarrow{u’}(x\prime ;y\prime )\]
\[\vec{u}=\overrightarrow{{{u}’}}\Leftrightarrow \left\{ \begin{matrix}
x={x}’ \\y={y}’ \\\end{matrix} \right.\]
Tọa độ một điểm:
Với mỗi điểm \[M\] trong mặt phẳng tọa độ thì tọa độ của vec tơ \[\overrightarrow{OM}\] được gọi là tọa độ của điểm \[M\].
\[\overrightarrow{OM}=x\vec{i}+y\vec{j}\Leftrightarrow M(x;y)\]
Liên hệ giữa tọa độ của điểm và của vectơ:
cho hai điểm \[A({{x}_{A}},y{}_{A});B({{x}_{B}},{{y}_{B}})\]
Ta có \[\overrightarrow{AB}({{x}_{B}}-{{x}_{A}};{{y}_{B}}-{{y}_{A}})\]
Tọa độ của vec tơ thì bằng tọa độ của điểm ngọn trừ đi tọa độ tương ứng của điểm đầu.
Tọa độ của tổng, hiệu ,tích của một số với một vectơ:
Cho hai vec tơ \[\overrightarrow{u}({{u}_{1}};{{u}_{2}});\overrightarrow{v}({{v}_{1}};{{v}_{2}})\]
Ta có
\[\overrightarrow{u}+\overrightarrow{v}=({{u}_{1}}+{{v}_{1}};{{u}_{2}}+{{v}_{2}})\]
\[\overrightarrow{u}-\overrightarrow{v}=({{u}_{1}}-{{v}_{1}};{{u}_{2}}-{{v}_{2}})\]
\[k\overrightarrow{u}=(k{{u}_{1}};k{{u}_{2}})\]
Tọa độ của trung điểm của đoạn thẳng và tọa độ trọng tâm của tam giác:
Tọa độ trung điểm:
Cho hai điểm \[A({{x}_{A}},{{y}_{A}});B({{x}_{B}},{{y}_{B}})\] tọa độ của trung điểm \[I({{x}_{I}};{{y}_{I}})\] được tính theo công thức:
\[\left\{ \begin{matrix}{{x}_{I}}=\frac{{{x}_{A}}+{{x}_{B}}}{2} \\{{y}_{I}}=\frac{{{y}_{A}}+{{y}_{B}}}{2} \\\end{matrix} \right.\]
Tọa độ trọng tâm:
Tam giác \[ABC\] có \[3\] đỉnh \[A({{x}_{A}},{{y}_{A}});B({{x}_{B}},{{y}_{B}});C({{x}_{C}};{{y}_{C}})\]. Trọng tâm \[G\] của tam giác có tọa độ:
\[\left\{ \begin{matrix}{{x}_{G}}=\frac{{{x}_{A}}+{{x}_{B}}+{{x}_{C}}}{3} \\{{y}_{G}}=\frac{{{y}_{A}}+{{y}_{B}}+{{y}_{C}}}{3}\\{{z}_{G}}=\frac{{{z}_{A}}+{{z}_{B}}+{{z}_{C}}}{3} \\\end{matrix} \right.\]
Trên đây là toàn bộ các nội dung về chủ đề vecto lớp 10. Mong rằng sẽ giúp các em chinh phục một phần nào chuyên đề này. Để xem thêm nhiều tài liệu hay hơn nữa về chuyên đề vecto, các em chọn các mục ở cuối bài viết này để xem chi tiết hơn.






