Tổng hợp các dạng bài tập hình học không gian lớp 11 và bí quyết học tốt
Trong chương trình Toán 11, hình học không gian là nội dung phức tạp làm khó không ít học sinh. Để giải các dạng toán hình này, các em cần nắm vững lý thuyết và có tư duy, trí tưởng tượng tốt. Tuy nhiên, các em cũng đừng quá lo lắng. Marathon Education sẽ chia sẻ cách giải các dạng bài tập hình học không gian lớp 11 và bí quyết giúp các em học hình học không gian hiệu quả.
>>> Xem thêm: Bỏ Túi 5 Phương Pháp Giúp Học Tốt Hóa 11
>>> Xem thêm: Học Online Toán 11 Bứt Phá Điểm Số Với Marathon Education
Tổng hợp các dạng bài tập hình học không gian lớp 11

Nắm vững các lý thuyết hình học không gian 11 (Nguồn: Internet)
Nắm vững lý thuyết hình học không gian lớp 11 sẽ giúp các em vẽ hình không gian đúng cũng như vận dụng làm các bài tập. Team Marathon Education đã tổng hợp lại 13 dạng bài tập hình học không gian thường gặp và phương pháp giải:
Dạng 1: Tìm giao tuyến của 2 mặt phẳng
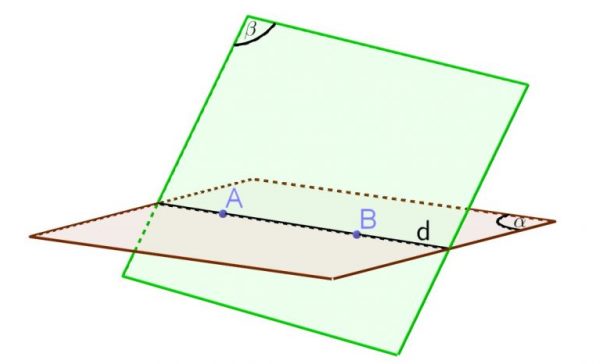
Giao tuyến của hai mặt phẳng (Nguồn: Internet)
Cách 1: Các em hãy tìm 2 điểm chung của hai mặt phẳng:
- Điểm chung thứ nhất có thể nhận biết rất dễ dàng.
- Điểm chung thứ hai là giao điểm của 2 đường thẳng còn lại, không đi qua điểm chung thứ nhất.
Cách 2: Nếu 2 mặt phẳng có chứa 2 đường thẳng song song thì các em chỉ cần tìm một điểm chung. Khi đó, giao tuyến sẽ đi qua điểm chung đó đồng thời song song với 2 đường thẳng này.
Dạng 2: Tìm giao điểm của đường thẳng và một mặt phẳng
Trong mặt phẳng (P), các em tìm giao điểm của a với một đường thẳng b nào đó.
Trường hợp không thấy đường thẳng b, các em thực hiện như sau:
- Trước tiên, các em hãy tìm một mặt phẳng (Q) có chứa a.
- Sau đó, các em tìm giao tuyến b của mặt phẳng (P) và (Q).
- Gọi A là giao điểm của 2 đường thẳng a và b, ta có A = a ∩ (P).
Dạng 3: Chứng minh 3 điểm thẳng hàng
Để chứng minh 3 điểm thẳng hàng, các em chỉ cần chứng minh các điểm ấy thuộc 2 mặt phẳng phân biệt.
Dạng 4: Chứng minh 3 đường thẳng đồng quy
Cách 1: Với 3 đường thẳng a, b, c, các em hãy chứng minh giao điểm của hai đường thẳng này là điểm chung của 2 mặt phẳng mà giao tuyến chính là đường thẳng thứ 3.
- Tìm A = a ∩ b
- Tìm 2 mặt phẳng (P), (Q) chứa A mà (P) ∩ (Q) = c
Cách 2: Các em có thể chứng minh các đường thẳng a, b, c không cùng nằm trên một mặt phẳng và cắt nhau theo từng đôi một.
Dạng 5: Tìm tập hợp giao điểm M của 2 đường thẳng di động a và b
- Tìm mặt phẳng (P) cố định có chứa đường thẳng a
- Tìm mặt phẳng (Q) cố định có chứa đường thẳng b
- Tìm đường thẳng c = (P) ∩ (Q). Ta có M thuộc c
- Giới hạn
Dạng 6: Dựng thiết diện của mặt phẳng (P) và khối đa diện T
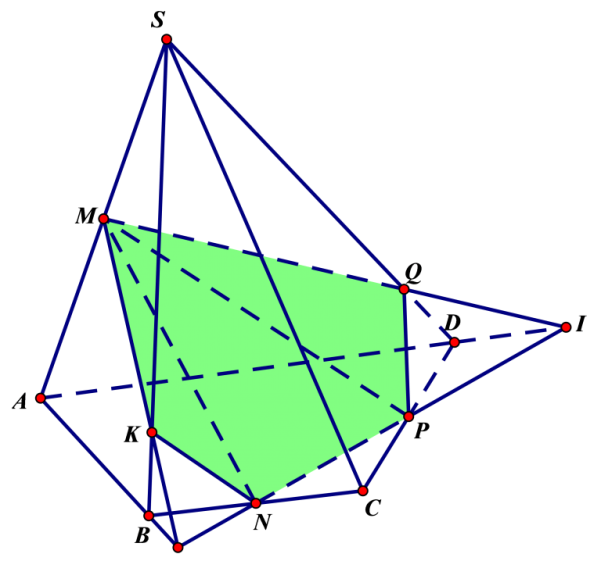
Thiết diện của mặt phẳng (P) và khối đa diện T (Nguồn: Internet)
Trọng dạng toán hình học không gian lớp 11 này, nếu các em muốn tìm thiết diện của mặt phẳng (P) và khối đa diện T thì hãy tìm giao tuyến của (P) với các mặt của T. Cụ thể:
Bước 1: Từ các điểm chung có sẵn, các em hãy xác định giao tuyến đầu tiên của mặt phẳng (P) với một mặt của khối đa diện (T).
Bước 2: Các em kéo dài giao tuyến và tìm giao điểm với các cạnh của mặt này. Làm tương tự để tìm được các giao tuyến còn lại thì sẽ dựng được thiết diện.
Dạng 7: Chứng minh đường thẳng a đi qua một điểm cố định
Các em hãy chứng minh: a = (P) ∩ (Q) với (P) là một mặt phẳng cố định. Mặt phẳng (Q) di động quanh đường thẳng cố định b. Lúc này, đường thẳng a sẽ đi qua: I = (P) ∩ b.
Dạng 8: Chứng minh 2 đường thẳng song song
Cách 1: Các em chứng minh đường thẳng a và b đồng phẳng, sau đó áp dụng các phương pháp như định lý Talet, đường trung bình,… để chứng minh đường thẳng a và đường thẳng b song song.
Cách 2: Các em chứng minh đường thẳng a và b cùng song song với đường thẳng thứ 3.
Cách 3: Các em hãy áp dụng định lý về giao tuyến đã học: Nếu 2 mặt phẳng cắt nhau và lần lượt chứa 2 đường thẳng song song cho trước thì giao tuyến của chúng cùng phương với 2 đường thẳng ấy.
Dạng 9: Tìm góc giữa 2 đường thẳng a và b chéo nhau
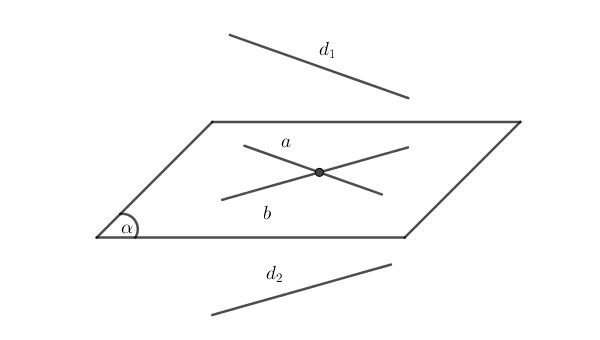
Góc giữa 2 đường thẳng chéo nhau (Nguồn: Internet)
- Các em hãy lấy một điểm O tùy ý.
- Qua điểm O này, dựng đường thẳng c song song với a và đường thẳng d song song với b.
- Góc nhọn được tạo bởi đường thẳng c và d chính là góc giữa 2 đường thẳng a và b.
- Các em lưu ý chọn điểm O thuộc đường thẳng a hoặc b và chỉ cần vẽ một đường thẳng song song với đường còn lại.
Dạng 10: Chứng minh một đường thẳng song song với mặt phẳng
Cách 1: Các em hãy chứng minh đường thẳng a song song với đường thẳng b thuộc mặt phẳng (P). Nếu không thấy đường thẳng b thì các em thực hiện các bước sau:
- Bước 1: Tìm mặt phẳng (Q) có chứa đường thẳng a.
- Bước 2: Tìm đường thẳng b = (P) ∩ (Q).
- Bước 3: Chứng minh đường thẳng b song song với đường thẳng a.
Cách 2: Các em hãy chứng minh đường thẳng a thuộc mặt phẳng (Q) song song với mặt phẳng (P).
Dạng 11: Dựng thiết diện song song với đường thẳng a cho trước
Để giải dạng toán này, các em hãy áp dụng tính chất sau “Một mặt phẳng song song với đường thẳng a nếu cắt một mặt phẳng nào đó có chứa a, thì sẽ cắt theo giao tuyến song song với a”.
Dạng 12: Chứng minh 2 mặt phẳng song song
Các em hãy chứng minh mặt phẳng này chứa 2 đường thẳng cắt nhau và song song với 2 đường thẳng cắt nhau nằm trong mặt phẳng còn lại.
Dạng 13: Tìm thiết diện được cắt bởi một mặt phẳng song song với một mặt phẳng cho trước
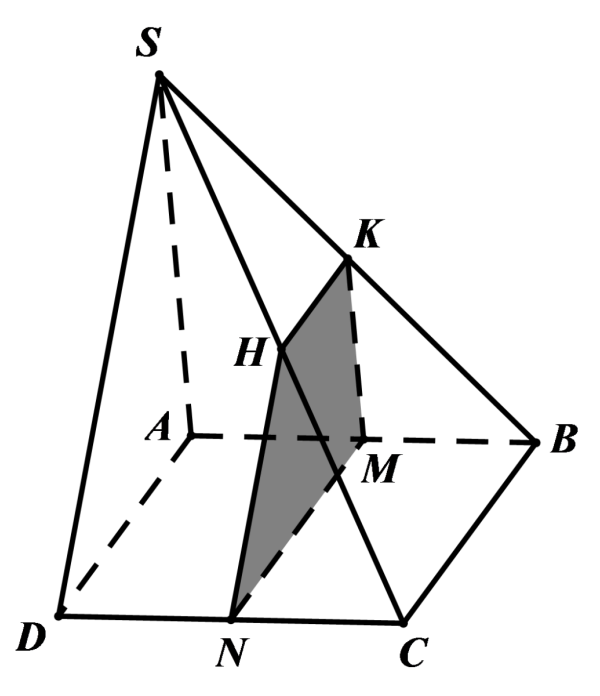
Thiết diện được cắt bởi một mặt phẳng song song với một mặt phẳng cho trước (Nguồn: Internet)
Để làm được bài tập dạng này, các em hãy dựa vào định lý “Nếu 2 mặt phẳng song song bị cắt bởi một mặt phẳng thứ 3 thì 2 giao tuyến song song với nhau”.
Tóm lại, để học tốt hình học không gian lớp 11, các em cần nắm chắc các định nghĩa, định lý và công thức từng dạng bài. Bên cạnh đó, các em cũng nên vận dụng lý thuyết để giải các bài tập cơ bản và nâng cao một cách hiệu quả.
Biết cách tưởng tượng và vẽ hình chính xác

Biết cách tưởng tượng và vẽ hình chính xác (Nguồn: Internet)
Để giải các bài tập hình học không gian lớp 11, trước tiên các em cần vẽ hình chính xác. Nếu hình vẽ sai thì các em khó có thể làm được bài, hoặc nếu làm được thì bài cũng không được tính điểm. Khi nhìn vào hình, các em hãy tưởng tượng để biết mặt phẳng nào nhìn thấy thì vẽ nét liền và mặt phẳng nào bị che khuất thì vẽ nét đứt. Một lưu ý khác cho các em là nên vẽ hình trước bằng bút chì để tránh sai sót.
Làm nhiều các dạng bài tập khác nhau
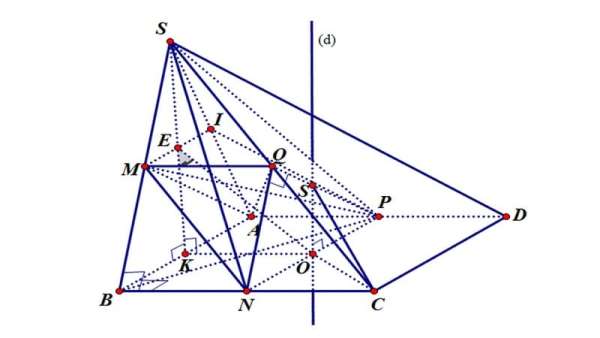
Làm nhiều dạng bài tập khác nhau (Nguồn: Internet)
Bên cạnh lý thuyết, việc luyện tập sẽ giúp các em thông thạo hình học không gian lớp 11. Các em không nên học tràn lan mà hãy học theo các dạng bài để tránh nhầm lẫn. Chỉ cần học tập chăm chỉ, kiên trì và không bỏ cuộc trước bất kỳ một bài Toán nào thì hình học không gian sẽ không còn là nội dung có thể làm khó các em.
>>> Xem thêm: Bí Quyết Học Tốt Toán 12 Và Đạt Điểm Cao Trong Kỳ Thi Đại Học
Đọc thêm sách tham khảo và Internet

Đọc thêm sách tham khảo và Internet (Nguồn: Internet)
Trước khi học hình học không gian lớp 11, các em cần trang bị đầy đủ sách giáo khoa, sách bài tập. Bên cạnh đó, các em nên đọc thêm các tài liệu hướng dẫn giải hình học không gian như sách tham khảo, mạng Internet. Tất nhiên, các tài liệu tham khảo cần phải được chọn lọc cẩn thận. Các em chỉ nên đọc tài liệu chính thống và phù hợp với nội dung học.
Tham khảo ngay các khoá học online của Marathon Education
Marathon Education đã chia sẻ những dạng bài tập hình học không gian lớp 11 và bí quyết học tốt qua bài viết trên. Hy vọng sau khi đọc xong, các em có thể tự tin hơn khi học nội dung này. Nếu các em thường xuyên rèn luyện cách vẽ hình và giải nhiều bài tập thì hình học không gian không còn là môn học “khó nhằn”.
Hãy liên hệ ngay với Marathon để được tư vấn nếu các em có nhu cầu học trực tuyến nâng cao kiến thức nhé! Marathon Education chúc các em được điểm cao trong các bài kiểm tra và kỳ thi sắp tới!






