Tóm tắt kiến thức toán lớp 11 bài 1: Hàm số lượng giác
Tóm tắt kiến thức toán lớp 11 bài 1: Hàm số lượng giác
Dưới đây là bài tóm tắt kiến thức và hướng dẫn giải toán lớp 11 bài 1: Hàm số lượng giác, mà các bạn có thể tham khảo để học tốt hơn!


Tóm tắt kiến thức toán hình lớp 11 bài 1
Với bài này, các bạn cần nắm được các nội dung sau
I – ĐỊNH NGHĨA
1. Hàm số sin và hàm số côsin
a) Hàm số sin:
Quy tắc đặt tương ứng mỗi số thực x với số thực sin x
sin : R → R
x ↦ y = sin x
được gọi là hàm số sin, kí hiệu là y = sin x.
Tập xác định của hàm số sin là R.
b) Hàm số côsin:
Quy tắc đặt tương ứng mỗi số thực x với số thực cos x
cos : R → R
x ↦ y = cos x
được gọi là hàm số côsin, kí hiệu là y = cos x.
Tập xác định của hàm số côsin là R.
2. Hàm số tang và hàm số côtang
a) Hàm số tang:
Hàm số tang là hàm số được xác định bởi công thức
y = sinx / cosx (cos x ≠ 0)
Kí hiệu là y = tan x.
b) Hàm số côtang:
Hàm số côtang là hàm số được xác định bởi công thức
y = cosx / sinx (sin x ≠ 0)
Kí hiệu là y = cot x.
II – TÍNH CHẤT TUẦN HOÀN CỦA HÀM SỐ LƯỢNG GIÁC
Hàm số y = sin x được gọi là hàm số tuần hoàn với chu kì 2π.
Hàm số y = cos x được gọi là hàm số tuần hoàn với chu kì 2π.
Hàm số y = tan x và y = cot x cũng là những hàm số tuần hoàn với chu kì π.
III – SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM SỐ LƯỢNG GIÁC
1. Hàm số
y =
sin
x
– Xác định với mọi x ∈ R và -1 ≤ sin x ≤ 1
– Là hàm số lẻ
– Là hàm số tuần hoàn với chu kì 2π
– Hàm số y = sin x đồng biến trên đoạn [ 0 ; π/2 ] và nghịch biến trên đoạn [ π/2 ; π ]
– Tập giá trị của hàm số y = sin x là [ -1 ; 1 ]
2. Hàm số
y =
cos
x
– Xác định với mọi x ∈ R và -1 ≤ cos x ≤ 1
– Là hàm số chẵn
– Là hàm số tuần hoàn với chu kì 2π
Với mọi x ∈ R ta có đẳng thức
sin ( x + (π/2)) = cos x
Hàm số y = cos x đồng biến trên đoạn [π ; 0] trên và nghịch biến trên đoạn [0 ; π]
Tập giá trị của hàm số y = cos x là [-1 ; 1]
Đồ thị của các hàm số y = cos x, y = cos x được gọi chung là các đường hình sin.
3. Hàm số
y =
tan
x
– Có tập xác định là D = R \ {(π/2) + kπ, k ∈ Z}
– Là hàm số lẻ
– Là hàm số tuần hoàn với chu kì π
Hàm số y = tan x đồng biến trên nửa khoảng [0 ; π/2)
Tập giá trị của hàm số y = tan x là khoảng (-∞ ; +∞)
4. Hàm số
y =
cot
x
– Có tập xác định là D = R \ {kπ, k ∈ Z}
– Là hàm số lẻ
– Là hàm số tuần hoàn với chu kì π
Hàm số y = cot x nghịch biến trên khoảng (0 ; π)
Tập giá trị của hàm số y = cot x là khoảng (-∞ ; +∞)
Hướng dẫn giải bài tập toán lớp 11 bài 1
Bài tập trong sách: (sgk/17)
Câu 1:
Xác định các giá trị của x trên đoạn [-π ; (3π/2)] để hàm số y = tan x.
a) Nhận giá trị bằng 0 ; b) Nhận giá trị bằng 1 ;
c) Nhận giá trị dương ; d) Nhận giá trị âm.
Lời giải:
a) Nhận giá trị bằng 0

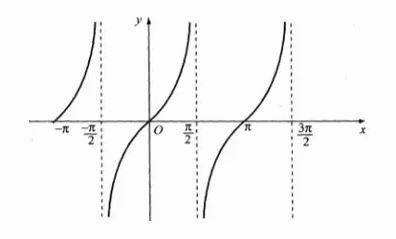
y = tan x = 0 tại các giá trị x = -π ; 0 ; π
b) Nhận giá trị bằng 1

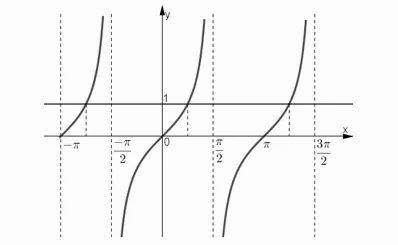
y = tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4
c) Nhận giá trị dương

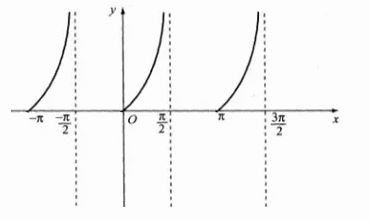
y = tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2)
d) Nhận giá trị âm

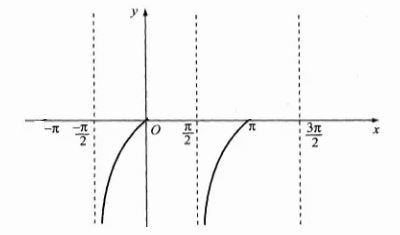
y = tan x < 0 với x ∈ [-π/2; 0) ∪ [π/2; π)
Nội Dung Chính
Câu 2:
Tìm tập xác định của các hàm số:
a) y = (1 + cos x)/ sin x ; b) y = (1 + cos x)/ sin x
c) y = tan(x – π/3) d) y = cot(x + π/6)
Lời giải:
a) Hàm số y = (1 + cos x)/ sin x xác định
⇔ sin x ≠ 0
⇔ x ≠ k.π (k ∈ Z)
Tập xác định của hàm số là D = R \ {kπ, k ∈ Z}
b) y = (1 + cos x)/ sin x

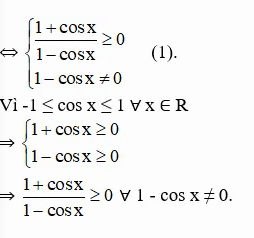
Do đó (1) ⇔ 1 – cos x ≠ 0 ⇔ cos x ≠ 1 ⇔ x ≠ k.2π
Vậy tập xác định của hàm số là D = R \ {k.2π, k ∈ Z}
c) y = tan(x – π/3)
⇔ x – π/3 ≠ π/2 +kπ (k ∈ Z)
⇔ x ≠ π/3 + π/2 +kπ
⇔ x ≠ 5π/6 +kπ
Vậy tập xác định của hàm số là D = R \ {5π/6 + kπ, k ∈ Z}
d) y = cot(x + π/6)
⇔ x + π/6 ≠ kπ (k ∈ Z)
⇔ x ≠ -π\6 + kπ
Vậy tập xác định của hàm số là D = R \ {-π/6 + kπ, k ∈ Z}
Câu 3:
Dựa vào đồ thị hàm số y = sin x, hãy vẽ đồ thị của hàm số y = ∣sin x∣.
Lời giải:
Đồ thị hàm số y = sin x
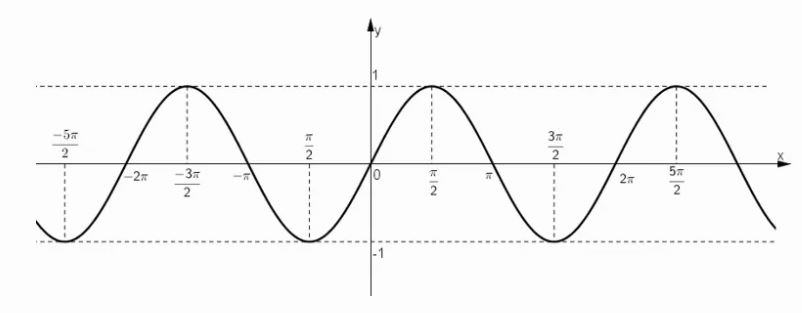
Ta có:

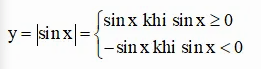
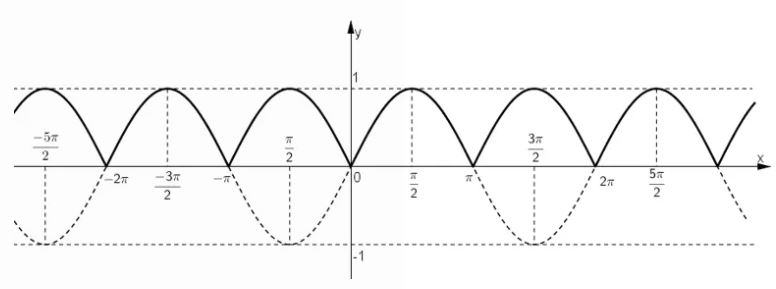
Vậy từ đồ thị hàm số y = sin x ta có thể suy ra đồ thị hàm số y = ∣sin x∣ bằng cách:
– Giữ nguyên phần đồ thị phía trên trục hoành (sin x >0)
– Lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành
Ta được đồ thị hàm số y = ∣sin x∣
Câu 4:
Chứng minh rằng sin 2(x + kπ) = sin 2x với mọi số nguyên k. Từ đó vẽ đồ thị hàm số y = sin 2x.
Lời giải:
sin 2x(x + kπ) = sin(2x + k2π) = sin2x (k ∈ Z)
(Do hàm số y = sin x có chu kì 2π)
⇒ Hàm số y = sin2x tuần hoàn với chu kì π
Hàm số y = sin2x là hàm số tuần hoàn với chu kì π và là hàm số lẻ.
Bảng biến thiên hàm số y = sin2x trên [-π/2 ; π/2]

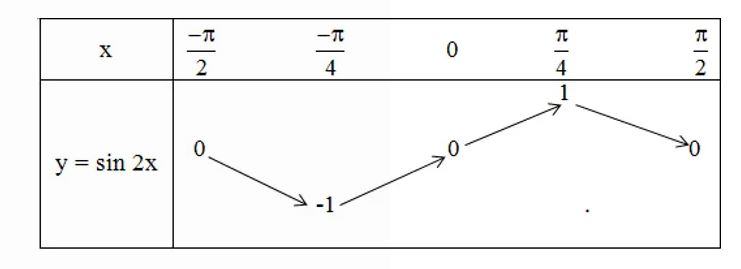
Đồ thị hàm số y = sin2x
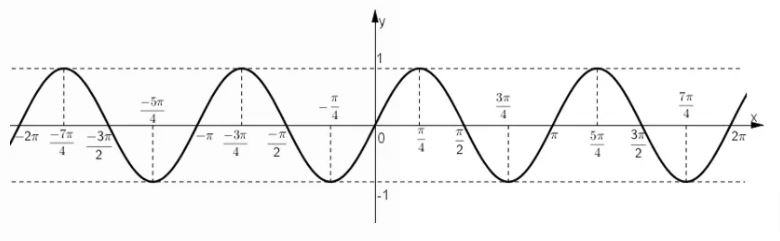
Câu 5:
Dựa vào đồ thị hàm số y = cos x, tìm các giá trị của x để cos x = ½.
Lời giải:
– Vẽ đồ thị hàm số y = cos x.
– Vẽ đường thẳng y = ½
– Xác định hoành độ các giao điểm.
Ta thấy đường thẳng y = ½ cắt đồ thị hàm số y = cos x tại các điểm có hoành độ π/3 + k.2π và -π/3 + k2π (k ∈ Z)
Vậy cos x = ½
⇔ x = ±π/3 + k2π (k ∈ Z)
Câu 6:
Dựa vào đồ thị hàm số y = sin x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương.
Lời giải:
Đồ thị hàm số y = sin x

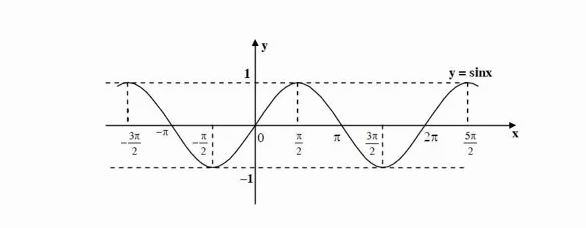
Từ đồ thị ta thấy: y = sin x > 0
⇔ x ∈ (-2π ; -π) ∪ (0 ;π) ∪ (2π ; 3π) ∪ …
hay x ∈ (k2π ; π + k2π) với (k ∈ Z)
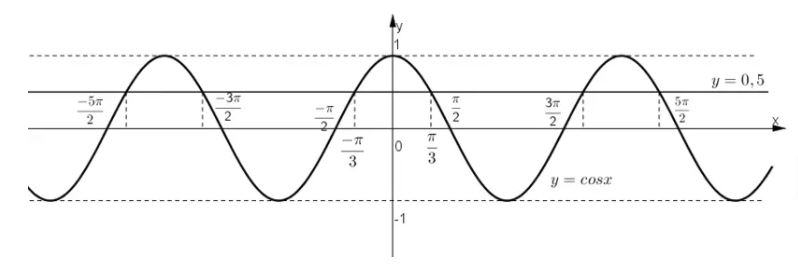
Câu 7:
Dựa vào đồ thị hàm số y = cos x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm.
Lời giải:
Đồ thị hàm số y = cos x

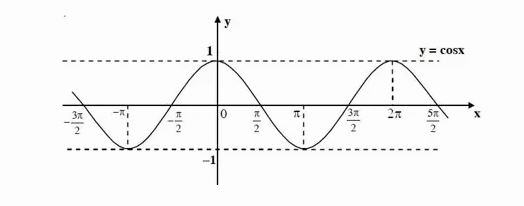
Từ đồ thị ta thấy: y = cos x < 0
⇔ x ∈ … ∪ (-3π/2 ; -π/2) ∪ (π/2 ; 3π/2) ∪ (5π/2 ; 7π/2) ∪ …
hay x ∈ (π/2 + k2π ; 3π/2 + k2π) với (k ∈ Z)
Câu 8:
Tìm giá trị lớn nhất của các hàm số:
a) y = 2√(cosx) +1
b) y = 3 – 2sinx
Lời giải:
a) Ta có:
0 ≤ √(cosx) ≤ 1
⟺ 0 ≤ 2√(cosx) ≤ 2
⟺ 1 ≤ 2√(cosx) +1 ≤ 3
hay 1 ≤ y ≤ 3
Vậy hàm số đạt giá trị lớn nhất bằng 3.
b) Ta có:
1 ≤ sinx ≤ 1
⟺ -2 ≤ -2sinx ≤ 2
⟺ 1 ≤ 3 – 2sinx ≤ 5
hay 1 ≤ y ≤ 5
Vậy hàm số đạt giá trị lớn nhất bằng 5.
Đó là tóm tắt kiến thức và hướng dẫn giải toán lớp 11 bài 1: Hàm số lượng giác, các bạn có thể tham khảo. Đừng quên xem thêm các bài giải toán khác tại chuyên mục : Toán Học lớp 11.
Share this:
We on social :






