PHƯƠNG PHÁP CHỌN MẪU TRONG NGHIÊN CỨU MARKETING – ppt κατέβασμα
Παρουσίαση με θέμα: “PHƯƠNG PHÁP CHỌN MẪU TRONG NGHIÊN CỨU MARKETING”— Μεταγράφημα παρουσίασης:
1
PHƯƠNG PHÁP CHỌN MẪU TRONG NGHIÊN CỨU MARKETING
3 chương

2
MỤC TIÊU CHƯƠNG 3 Hiểu được các khái niệm cơ bản về chọn mẫu
Giải thích được vì sao phải chọn mẫu trong nghiên cứu Phân biệt được các phương pháp chọn mẫu Biết quy trình lấy mẫu gồm các bước gì Có thể thực hành việc lấy mẫu cho cuộc nghiên cứu

3
Nội dung chương 3.1 Các khái niệm cơ bản về chọn mẫu
3.2 Lợi ích của việc chọn mẫu 3.3 Hạn chế của việc chọn mẫu 3.4 Các phương pháp chọn mẫu 3.5 Quy trình chọn mẫu

4
3.1 Các khái niệm cơ bản về chọn mẫu
Tổng thể ( Population) Là tập hợp các phần tử mà nhà nghiên cứu cần nghiên cứu để thỏa mãn mục đích và phạm vi của đề tài nghiên cứu Một tổng thể được định nghĩa rõ ràng theo các phần tử, đơn vị lấy mẫu, quy mô và thời gian

5
3.1 Các khái niệm cơ bản về chọn mẫu(tt)
Ví dụ: Nhà nghiên cứu xác định đối tượng nghiên cứu là người tiêu dùng tại TpHCM có độ tuổi từ 18 đến 40 Vậy tổng thể là toàn bộ những người sinh sống tại TpHCM trong độ tuổi từ 18-40

6
3.1 Các khái niệm cơ bản về chọn mẫu(tt)
Tổng thể bộc lộ (vd: doanh nghiệp, người tiêu dùng 1 sp/dv) Tổng thể tiềm ẩn(vd: nhóm người ưa du lịch mạo hiểm, nhóm ủng hộ một chính sách…) Tổng thể đồng chất (các doanh nghiệp trong ngành dệt may…) Tổng thể không đồng chất (vd toàn bộ doanh nghiệp tại TpHCM)

7
3.1 Các khái niệm cơ bản về chọn mẫu(tt)
Mẫu ( Sample) Là một tập hợp những phần tử lấy ra từ một tổng thể Nghiên cứu trên mẫu nhằm tìm ra những tính chất, những phản ứng với một xử lý thử nghiệm Kết quả nghiên cứu của mẫu dùng suy diễn cho cả tổng thể

8
3.1 Các khái niệm cơ bản về chọn mẫu(tt)
Lấy mẫu hay chọn mẫu (sampling) Lấy mẫu hay chọn mẫu là một công việc được tiến hành một cách khoa học để mẫu được chọn có đủ những tính chất điển hình của tổng thể Việc lấy mẫu sai sẽ dẫn đến những nhận định sai về tổng thể mà ta nghiên cứu Việc lấy mẫu giúp nhà nghiên cứu rút ra những chẩn đoán thông qua mô tả những đặc điểm chung của tổng thể

9
3.1 Các khái niệm cơ bản về chọn mẫu(tt)

10
3.1 Các khái niệm cơ bản về chọn mẫu(tt)
Khung chọn mẫu ( Sample Flame) Là danh sách liệt kê dữ liệu cần thiết của tất cả các đơn vị hay phần tử của tổng thể Xác định khung chọn mẫu là một công việc khó khăn Xác định khung chọn mẫu thông qua dữ liệu thứ cấp hoặc tiến hành phỏng vấn

11
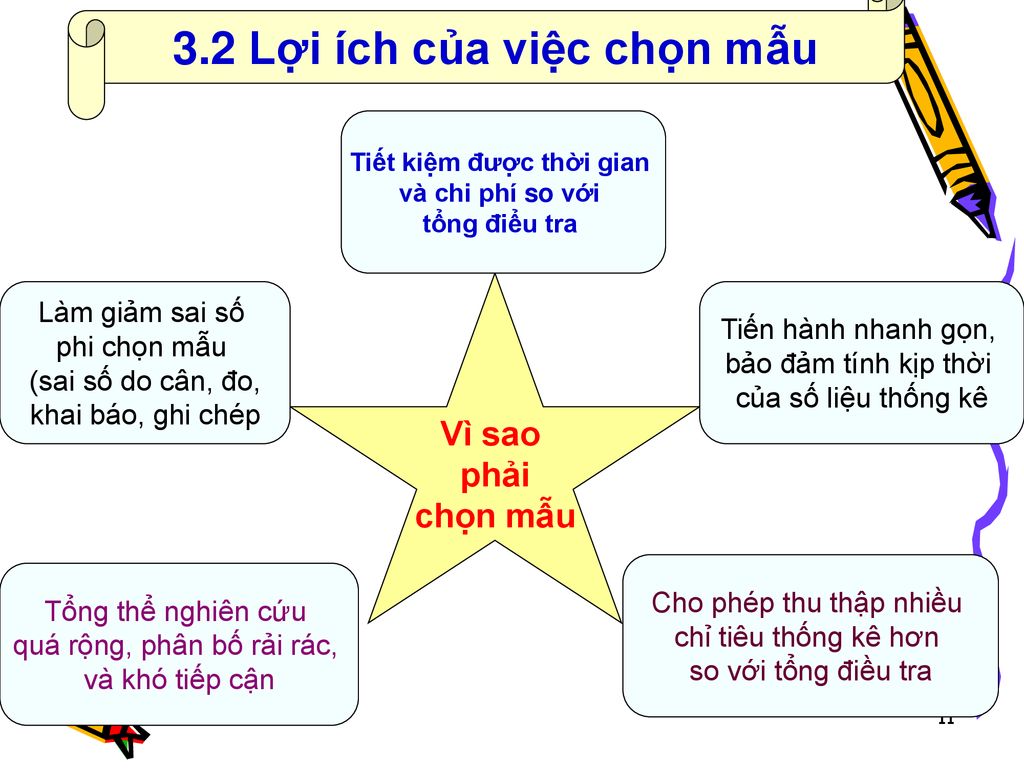
3.2 Lợi ích của việc chọn mẫu Tiết kiệm được thời gian
và chi phí so với tổng điểu tra Vì sao phải chọn mẫu Làm giảm sai số phi chọn mẫu (sai số do cân, đo, khai báo, ghi chép Tiến hành nhanh gọn, bảo đảm tính kịp thời của số liệu thống kê Cho phép thu thập nhiều chỉ tiêu thống kê hơn so với tổng điều tra Tổng thể nghiên cứu quá rộng, phân bố rải rác, và khó tiếp cận
12
3.3 Hạn chế của chọn mẫu Tồn tại “Sai số chọn mẫu“
Kết quả cuộc nghiên cứu không thể tiến hành phân nhỏ theo mọi phạm vi và tiêu thức nghiên cứu như điều tra toàn bộ

13
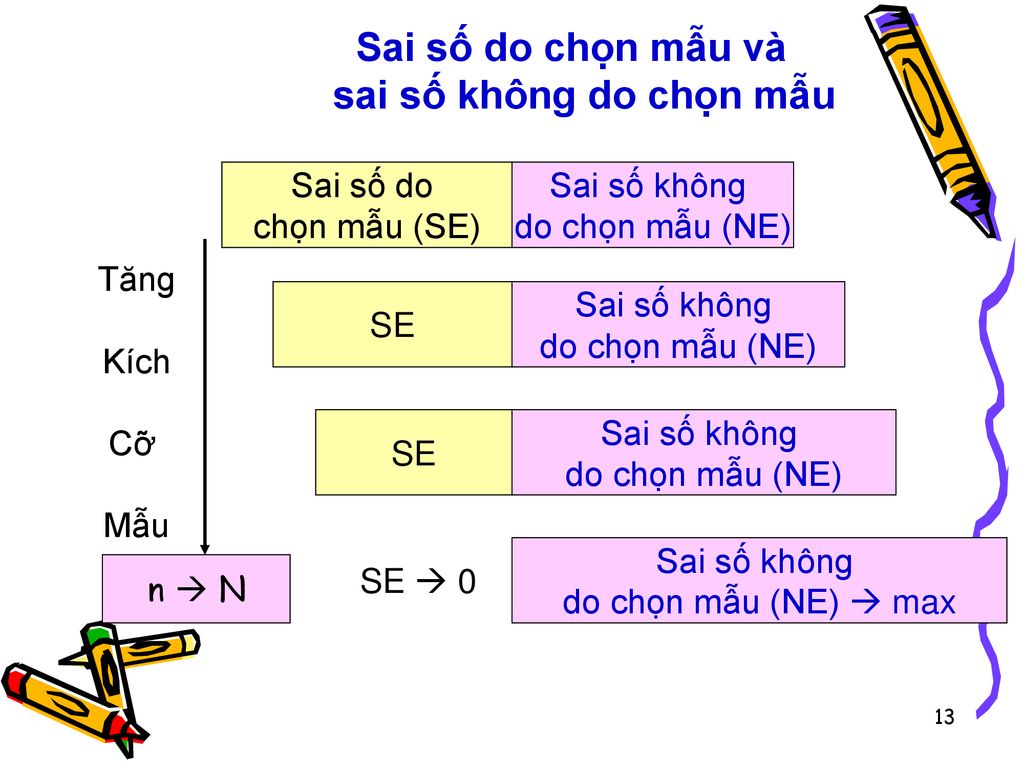
Sai số do chọn mẫu và sai số không do chọn mẫu
chọn mẫu (SE) Sai số không do chọn mẫu (NE) Tăng Kích Cỡ Mẫu SE Sai số không do chọn mẫu (NE) SE Sai số không do chọn mẫu (NE) SE 0 Sai số không do chọn mẫu (NE) max n N
14
3.4 Các phương pháp chọn mẫu
Hai phương pháp chọn mẫu Chọn mẫu theo xác suất Chọn mẫu phi xác suất Ngẫu nhiên đơn giản Hệ thống Phân tầng Theo cụm Thuận tiện Theo phán đoán Định mức Tích lũy

15
So sánh chọn mẫu theo xác suất và phi xác suất
Ưu điểm Tính đại diện cao Khái quát hóa cho tổng thể Tiết kiệm thời gian và chi phí Nhược điểm Tốn kém thời gian và chi phí Tính đại diện thấp Phạm vi áp dụng Nghiên cứu mô tả NC định lượng Nghiên cứu thăm dò Nghiên cứu định tính

16
Chọn mẫu ngẫu nhiên đơn giản
Chọn mẫu theo xác suất Phải có danh sách đơn vị tổng thể Rút thăm, quay số, dùng bảng số ngẫu nhiên nếu tổng thể lớn Dùng máy tính để chọn – Ví dụ: kiểm tra chất lượng sản phẩm trong dây chuyền sản xuất hàng loạt Chọn mẫu ngẫu nhiên đơn giản

17
Chọn mẫu theo xác suất (tt)
Chuẩn bị danh sách đơn vị lấy mẫu Tính bước nhảy (khoảng cách) k dựa vào N và n (k= N/n) Chọn ngẫu nhiên mẫu đầu tiên Lần lượt lấy các mẫu tiếp theo dựa vào bước nhảy Chọn mẫu hệ thống

18
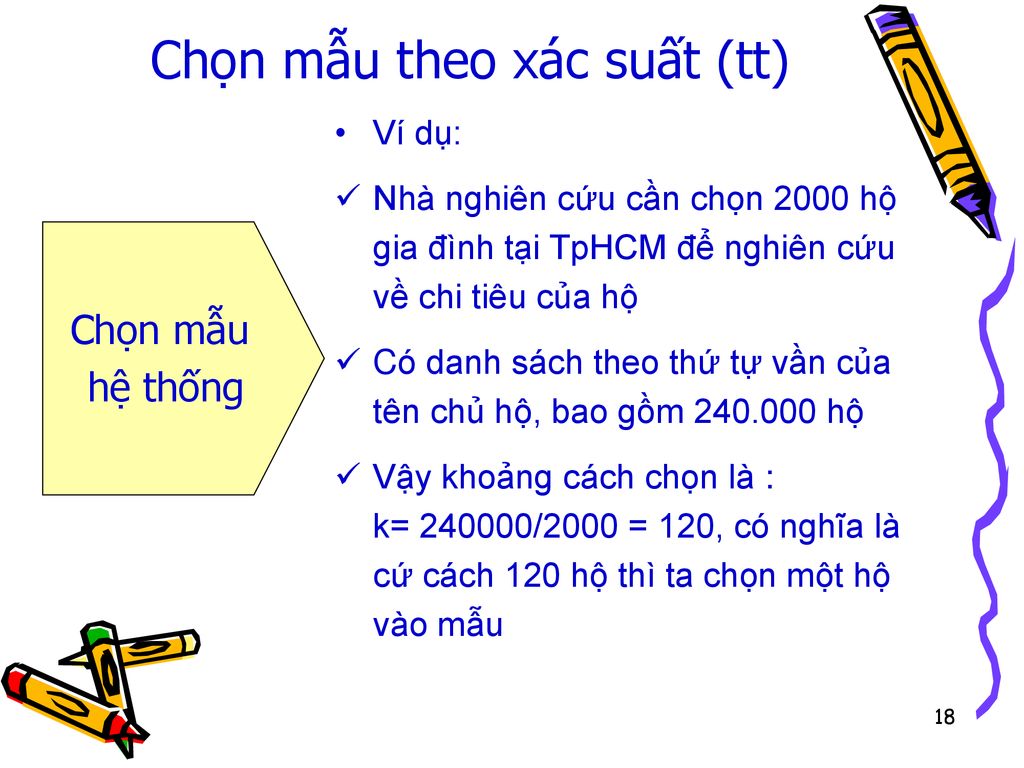
Chọn mẫu theo xác suất (tt)
Ví dụ: Nhà nghiên cứu cần chọn 2000 hộ gia đình tại TpHCM để nghiên cứu về chi tiêu của hộ Có danh sách theo thứ tự vần của tên chủ hộ, bao gồm hộ Vậy khoảng cách chọn là : k= /2000 = 120, có nghĩa là cứ cách 120 hộ thì ta chọn một hộ vào mẫu Chọn mẫu hệ thống
19
Chọn mẫu theo xác suất (tt)
Phổ biến nhất vì tính chính xác & đại diện cao Chia tổng thể ra từng nhóm nhỏ theo 1 tiêu thức nào đó (thu nhập, giới tính, tuổi tác, trình độ văn hóa,…) Chọn ngẫu nhiên hay hệ thống trong từng nhóm phân tầng theo tỉ lệ với độ lớn của nhóm Chọn mẫu phân tầng

20
Chọn mẫu theo xác suất (tt)
Ví dụ: Một toà soạn báo muốn tiến hành nghiên cứu một mẫu 1000 doanh nghiệp trên cả nước về sự quan tâm của họ đối với tờ báo nhằm tiếp thị việc đưa thông tin quảng cáo trên báo Toà soạn có thể căn cứ vào các tiêu thức: vùng địa lý (miền Bắc, miền Trung, miền Nam) ; hình thức sở hữu (quốc doanh, ngoài quốc doanh, công ty 100% vốn nước ngoài,…) để quyết định cơ cấu của mẫu nghiên cứu Chọn mẫu phân tầng

21
Chọn mẫu theo xác suất (tt)
Lập danh sách tổng thể chung theo từng khối (như quận-huyện, xã-phường, lượng sản phẩm sản xuất trong 1 khoảng thời gian…) Áp dụng phương pháp này khi không có sẵn danh sách đầy đủ các đơn vị trong tổng thể cần nghiên cứu Chọn mẫu theo khối/ theo cụm

22
Chọn mẫu theo xác suất (tt)
Sử dụng phương pháp ngẫu nhiên đơn giản hay phương pháp hệ thống để chọn mẫu Mẫu có thể được lấy ra từ 1 nhóm, (one- stage cluster sampling) Mẫu có thể được lấy ra từ các nhóm (two – stage cluster sampling) Chọn mẫu theo khối/ theo cụm
23
Chọn mẫu theo xác suất (tt)
Ví dụ: Tổng thể chung là sinh viên của một trường đại học. Khi đó ta sẽ lập danh sách các lớp chứ không lập danh sách sinh viên, tiếp theo chọn ra các lớp điều tra. Chọn mẫu theo khối/ theo cụm

24
Chọn mẫu phi xác suất Chọn mẫu thuận tiện
Dựa trên tính “dễ tiếp xúc” và “cơ hội thuận tiện” để chọn mẫu Chỉ dùng cho nghiên cứu thăm dò, trắc nghiệm, Không dùng cho nghiên cứu mô tả hay nhân quả vì tính đại diện không cao Chọn mẫu thuận tiện

25
Chọn mẫu phi xác suất(tt)
Ví dụ: Nhân viên điều tra có thể hỏi bất cứ người nào mà họ gặp ở trung tâm thương mại, đường phố, cửa hàng,.. để xin thực hiện cuộc phỏng vấn Nếu người được phỏng vấn không đồng ý thì họ chuyển sang đối tượng khác Chọn mẫu thuận tiện

26
Chọn mẫu phi xác suất(tt)
Phỏng vấn viên là người tự đưa ra phán đoán về đối tượng cần chọn vào mẫu Tính đại diện của mẫu phụ thuộc nhiều vào kinh nghiệm và sự hiểu biết của người tổ chức việc điều tra và cả người đi thu thập dữ liệu. Chọn mẫu theo phán đoán

27
Chọn mẫu phi xác suất(tt)
Ví dụ Nhân viên phỏng vấn được yêu cầu đến các trung tâm thương mại chọn các phụ nữ ăn mặc sang trọng để phỏng vấn Như vậy phỏng vấn viên không có tiêu chuẩn cụ thể “thế nào là sang trọng” mà hoàn toàn dựa vào phán đoán để chọn ra người cần phỏng vấn Chọn mẫu theo phán đoán

28
29
Chọn mẫu phi xác suất(tt)
Tổng thể rộng, sự khác biệt (biến động) giữa các phần tử không lớn Tổng thể đã được phân tổ nhóm trước (đồng nhất) Chỉ chọn cho đủ số lượng không cần ngẫu nhiên Dựa vào đặc tính kiểm soát (tiêu thức phân tổ) của từng nhóm để chọn Chọn mẫu theo định mức

30
Chọn mẫu phi xác suất(tt)
Ví dụ: Nhà nghiên cứu yêu cầu các vấn viên đi phỏng vấn 800 người có tuổi trên 18 tại 1 thành phố. Ta có chọn dựa theo 2 tiêu thức phân tổ như sau: Chọn 400 người (200 nam và 200 nữ) có tuổi từ 18 đến 40 Chọn 400 người (200 nam và 200 nữ) có tuổi từ 40 trở lên. Sau đó nhân viên điều tra có thể chọn những người gần nhà hay thuận lợi cho việc điều tra của họ để dễ nhanh chóng hoàn thành công việc. Chọn mẫu theo định mức

31
Chọn mẫu phi xác suất(tt)
Chọn một mẫu đầu tiên Các mẫu tiếp theo được chọn ra từ việc nhờ giới thiệu Áp dụng cho các nghiên cứu khá đặc biệt, mẫu khó tìm hoặc khó tiếp cận Chọn mẫu tích lũy/ phát triển mầm

32
Chọn mẫu phi xác suất(tt)
Ví dụ: Chúng ta cần nghiên cứu thị trường dụng cụ chơi golf tại TP.HCM và đối tượng để thu thập dữ liệu là những người chơi golf Chúng ta có thể chọn được một vài người chơi golf (chọn mầm) và nhờ những người này giới thiệu những người khác (phát triển mầm) tham gia vào mẫu Chọn mẫu tích lũy/ phát triển mầm

33
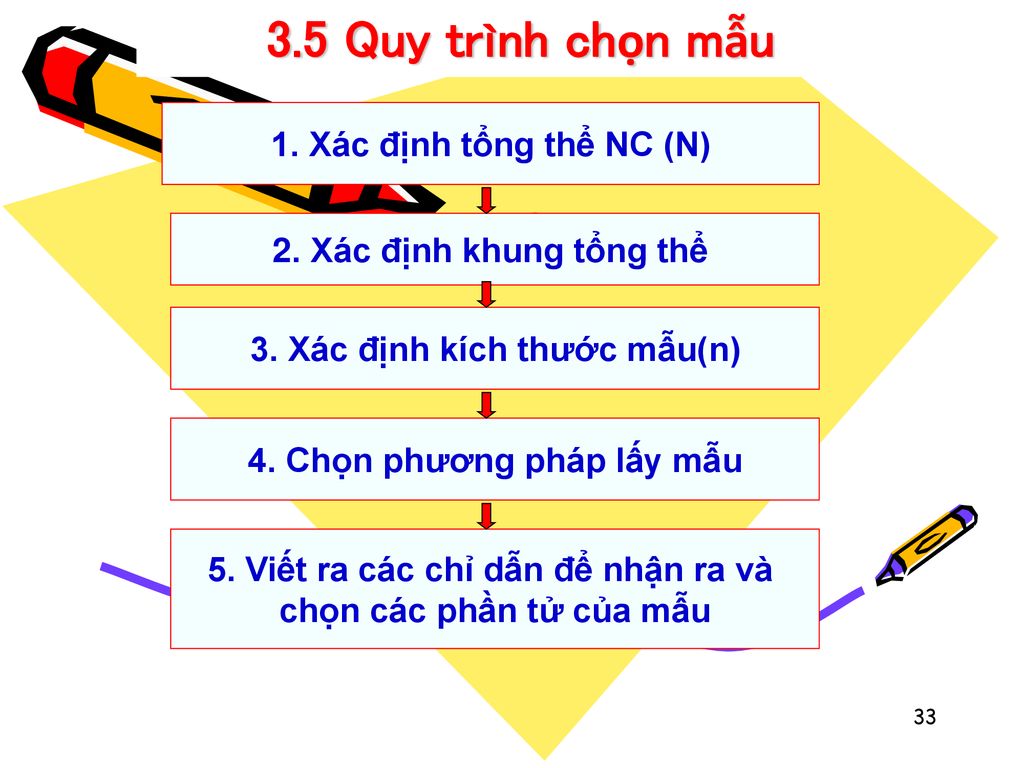
3.5 Quy trình chọn mẫu 1. Xác định tổng thể NC (N)
2. Xác định khung tổng thể 3. Xác định kích thước mẫu(n) 4. Chọn phương pháp lấy mẫu 5. Viết ra các chỉ dẫn để nhận ra và chọn các phần tử của mẫu
34
Xác định kích thước mẫu Xác định kích thước mẫu (qui mô mẫu hay cỡ mẫu) là xác định số lượng đơn vị điều tra trong tổng thể mẫu để tiến hành thu thập số liệu

35
Xác định kích thước mẫu(tt)
Việc xác định cỡ mẫu phụ thuộc vào: Mục tiêu nghiên cứu Yêu cầu của dữ liệu phân tích Hạn chế về thời gian Hạn chế về chi phí Cỡ mẫu tương quan với lớn của tổng thể Cỡ mẫu khi chọn mẫu phi xác suất

36
Xác định kích thước mẫu(tt)
Các phương pháp xác định cỡ mẫu Dựa theo kinh nghiệm điều tra thực tế Dựa theo cỡ mẫu của một cuộc điều tra tương tự Dựa theo kinh phí của cuộc nghiên cứu: Trong đó: C: Tổng kinh phí được cấp; Co: Kinh phí chi cho các khâu chuẩn bị, tập huấn nghiệp vụ thu thập, xử lý và các chi phí chung khác; Z: Chi phí cần thiết cho tất cả các khâu điều tra tính cho một đơn vị điều tra.

37
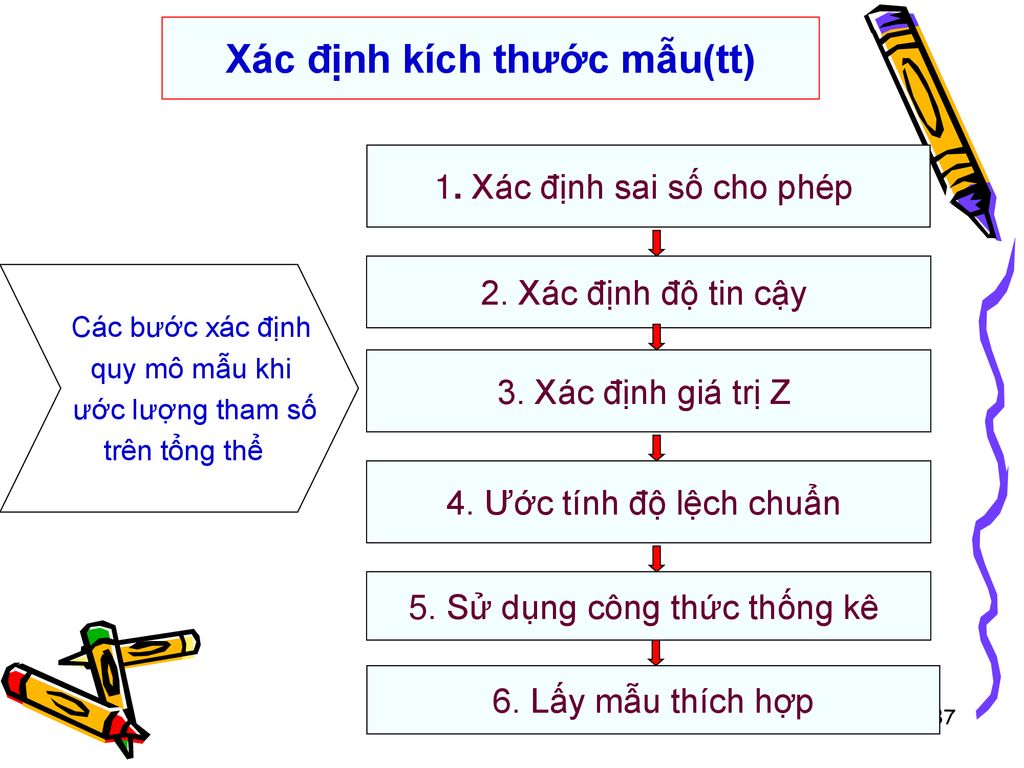
Xác định kích thước mẫu(tt)
1. Xác định sai số cho phép 2. Xác định độ tin cậy Các bước xác định quy mô mẫu khi ước lượng tham số trên tổng thể 3. Xác định giá trị Z 4. Ước tính độ lệch chuẩn 5. Sử dụng công thức thống kê 6. Lấy mẫu thích hợp
38
Xác định sai số cho phép Sai số cho phép/Dung sai E (Allowable Error)
Ví dụ 1: Điều tra thu nhập trung bình trên một địa bàn dân cư, ta muốn rằng ước lượng về thu nhập trung bình của mẫu sẽ nằm trong khoảng trên dưới đồng so với trị số trung bình thật của tổng thể nghiên cứu, khi đó E= ± Ví dụ 2: Điều tra mức tiêu thụ trung bình về bia, ta muốn rằng ước lượng về mức tiêu thụ trung bình về bia của mẫu nằm trong khỏang trên dưới 5% hay 0,05 so với trị số trung bình thật của tổng thể nghiên cứu, khi đó: E = ± 0,05

39
Xác định độ tin cậy và Z Trị số Z gắn với mức độ tin cậy
– Ví dụ: Chọn độ tin cậy (1- α) = 95% (Mức độ ý nghĩa α =5% = 0,05) Z = 1,96 – Vài trị số Z thường dùng (trích từ giáo trình thống kê) (1-α) Zα 90% 1.65 95% 1.96 97% 2.17 98% 2.33 99% 2.58

40
Xác định độ lệch chuẩn Thông thường ta không biết được phương sai tổng thể , do đó ta dùng 1 trong 3 cách sau: – Dựa vào kết quả nghiên cứu tương tự trước đây – Dựa vào kinh nghiệm và sự hiểu biết về tổng thể nghiên cứu để suy đoán. – Điều tra thử một mẫu có cỡ mẫu 30 đơn vị để tính phương sai mẫu theo công thức:

41
Công thức tính cỡ mẫu Trường hợp giá trị tham số của tổng thể là một số tuyệt đối

42
Công thức tính cỡ mẫu Khi các số đo là các số tỉ lệ hay bách phân (%)

43
CÂU HỎI THẢO LUẬN So sánh ưu nhược điểm của các phương pháp chọn mẫu theo xác suất. Cho ví dụ minh họa Trường hợp nào nhà nghiên cứu sử dụng các phương pháp chọn mẫu phi xác suất? Cho ví dụ minh họa. Giả sử một nhà nghiên cứu tiến hành dự án nghiên cứu về sự hài lòng của sinh viên trường Đại học Tài chính-Marketing. Theo bạn, nhà nghiên cứu có thể sử dụng phương pháp chọn mẫu nào? Giải thích câu trả lời của bạn. Với đề tài nghiên cứu nhóm bạn đã chọn ở chương 1, hãy hoạch định phương án chọn mẫu cho dự án nghiên cứu đó.

44
Thảo luận tại lớp Xác định đối tượng nghiên cứu của đề tài nhóm
Trình bày phương pháp chọn mẫu Các khó khăn trong việc tiếp cận đối tượng phỏng vấn và cách khắc phục?

45
Bài tập Công ty BAVIMILK chuyên về sản xuất các sản phẩm sữa. Công ty muốn xâm nhập thị trường sữa TPHCM. Họ yêu cầu phòng nghiên cứu thị trường thực hiện nghiên cứu về thị hiếu người tiêu dùng sữa tại TPHCM. Giả sử anh (chị) là nhân viên NCTT của công ty. Hãy lập kế hoạch nghiên cứu cho dự án trên

46
Tên đề tài Mục tiêu nghiên cứu Dữ liệu cần thu thập Nguồn dữ liệu Phương pháp chọn mẫu Phương pháp thu thập dữ liệu

47

48

49

50

51

52
THẢO LUẬN ĐỐI TƯỢNG NGHIÊN CỨU? PHƯƠNG PHÁP CHỌN MẪU?
CÁCH THỨC TIẾP CẬN? NHỮNG KHÓ KHĂN? Khắc phục?







