Hệ thống kiến thức Toán lớp 11 Giữa học kì 1

Hệ thống kiến thức Toán lớp 11 Giữa học kì 1 chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Toán 11 học kì 1. Mời các bạn cùng đón xem:

Hệ thống kiến thức Toán lớp 11 Giữa học kì 1

A. ĐẠI SỐ VÀ GIẢI TÍCH

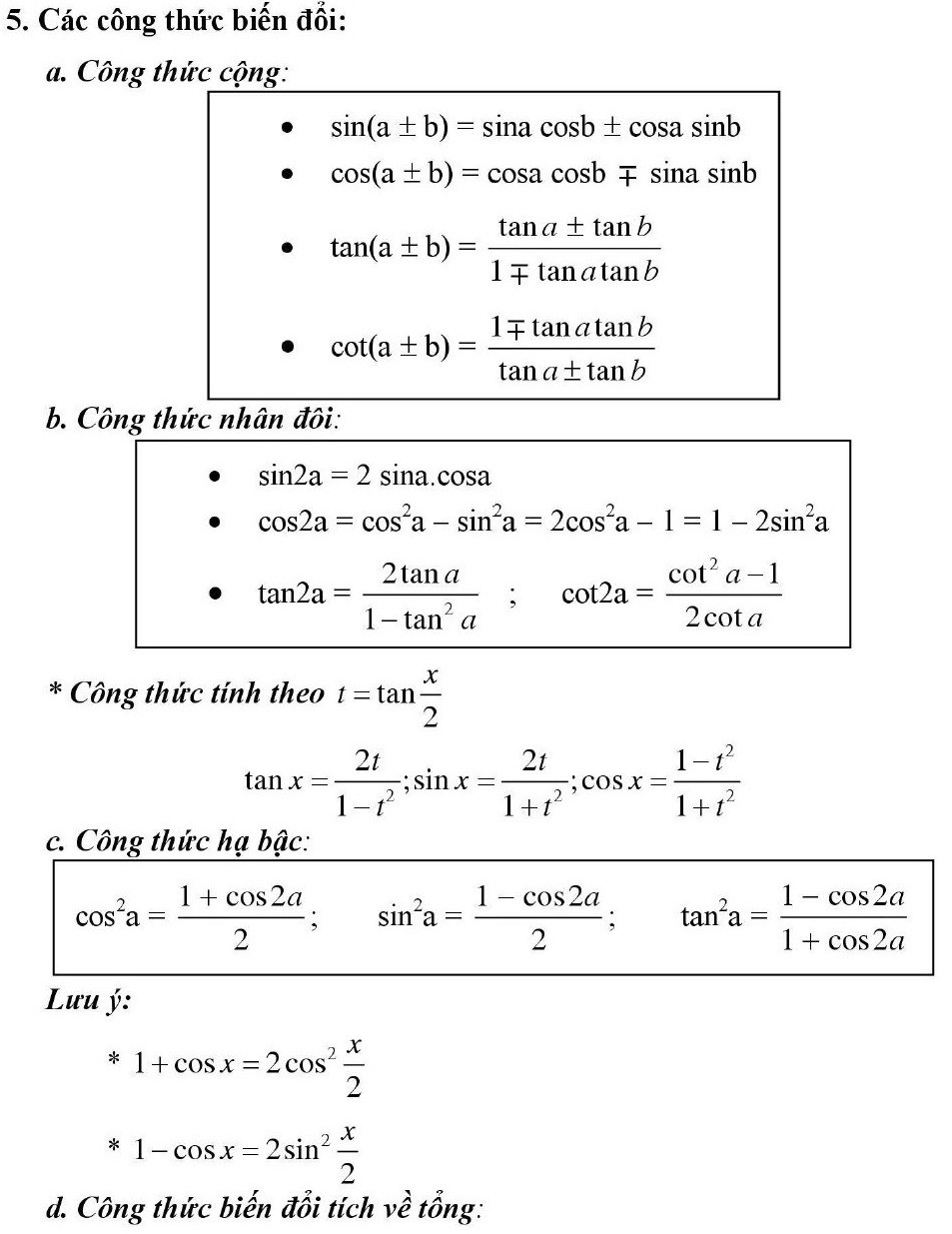
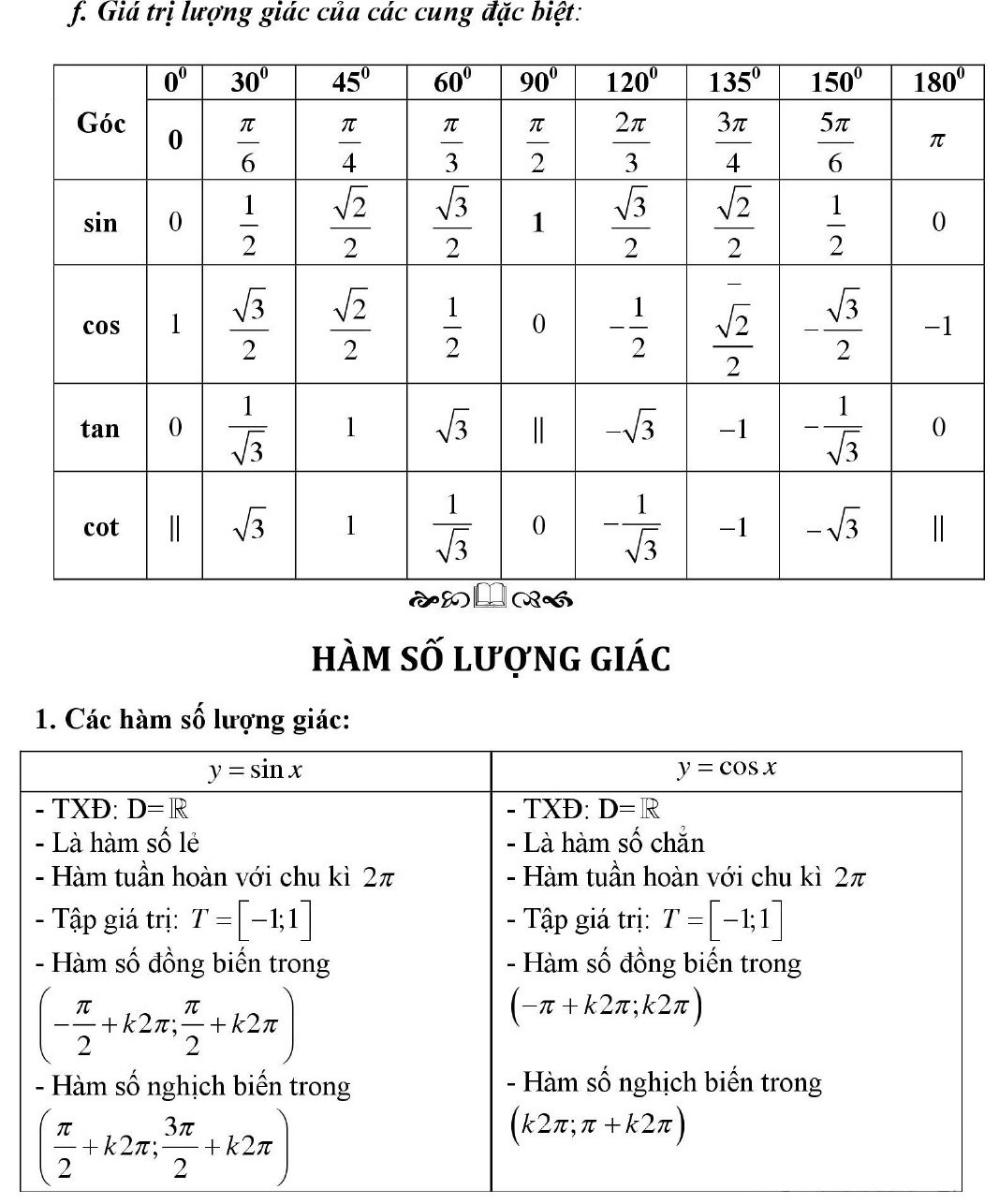
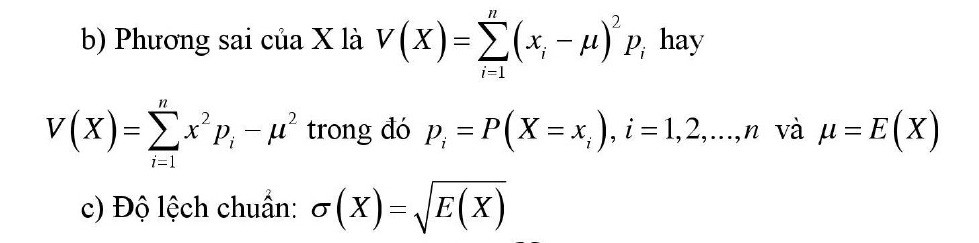
B. HÌNH HỌC

1. Định nghĩa phép biến hình

– Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.

– Nếu kí hiệu phép biến hình là F thì ta viết F(M) = M’ hay M’ = F(M) và gọi M’ là ảnh của điểm M qua phép biến hình F.

– Nếu ℋ  là một hình nào đó trong mặt phẳng thì ta kí hiệu ℋ ‘ = F(ℋ) là tập các điểm M’ = F(M), với mọi điểm M thuộc ℋ. Khi đó, ta nói F là biến hình ℋ  thành hình ℋ ‘, hay hình ℋ ‘ là ảnh của hình ℋ  qua phép biến hình F.

– Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.

Ví dụ. Cho trước đường thẳng d, với mỗi điểm M trong mặt phẳng, gọi M’ là điểm sao cho M’ đối xứng với M qua d.

Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên là một phép biến hình vì chỉ có duy nhất 1 điểm M’ thỏa mãn yêu cầu.

2. Định nghĩa phép tịnh tiến

– Định nghĩa: Trong mặt phẳng, cho vectơ v→. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho MM’→  =  v→ được gọi là phép tịnh tiến theo vectơ v→.

– Phép tịnh tiến theo vectơ  thường được kí hiệu là được gọi là vectơ tịnh tiến.

Vậy: Tv→ (M)=  M’ ⇔MM’→  =  v→.

– Phép tịnh tiến theo vectơ – không chính là phép đồng nhất.

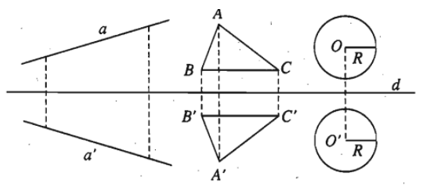
– Ví dụ 1. Cho hình vẽ sau:

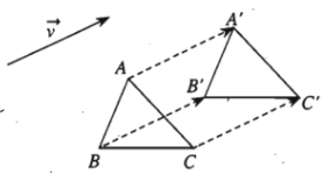
Ta có: Tv→ (A)=  A’ ;   Tv→ (B)=  B’ ;  Tv→ (C)=  C’ .

3. Tính chất của phép tịnh tiến

– Tính chất 1.  Nếu Tv→ (M)=  M’ ;  Tv→ (N)=  N’ thì M’N’ →  =  MN→ và từ đó suy ra M’N’ = MN.

Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.

– Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

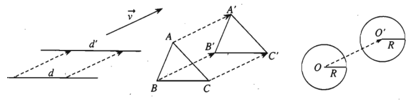
4. Biểu thức tọa độ của phép tịnh tiến

Trong mặt phẳng tọa độ Oxy cho vectơ v→ (a ;  b). Với mỗi điểm M(x ; y) ta có M’(x’ ; y’) là ảnh của điểm M qua tịnh tiến theo vectơ v→.

Khi đó:  

MM’→  =  v→  ⇔x’−x =ay’  − y=b ⇒x’=x +ay’  = y+b

đây chính là biểu thức tọa độ của phép tịnh tiến Tv→.

Ví dụ. Trong mặt phẳng tọa độ Oxy, cho điểm A(1 ; – 2). Phép tịnh tiến theo vectơ biến A thành điểm A’ có tọa độ là bao nhiêu?

Lời giải:

Gọi tọa độ điểm A’ = (x’; y’).

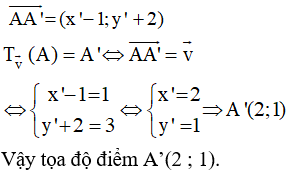
5. Định nghĩa của phép đối xứng trục

– Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

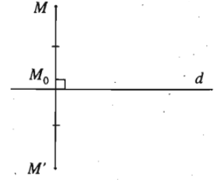
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản là trục đối xứng.

Phép đối xứng trục d thường được kí hiệu là Đd.

– Nếu hình ℋ ‘ là ảnh của hình ℋ  qua phép đối xứng trục d thì ta còn nói ℋ  đối xứng với ℋ ‘ qua d, hay ℋ  và ℋ ‘ đối xứng với nhau qua d.

– Nhận xét:

1) Cho đường thẳng d. Với mỗi điểm M, gọi M0 là hình chiếu vuông góc của M

trên đường thẳng d. Khi đó: M’ = Đd(M) ⇔ M0M’→  =  − M0M→

2) M’ = Đd(M) ⇔M = Đd(M’).

6. Biểu thức tọa độ của phép đối xứng trục

1) Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đd(M) = (x’ ; y’) thì x’  =  xy’  =  −y, đây là biểu thức tọa độ của phép đối xứng qua trục Ox. 

2) Chọn hệ trục tọa độ Oxy sao cho trục Oy trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đd(M) = (x’; y’) thì x’  =  −xy’  = y, đây là biểu thức tọa độ của phép đối xứng qua trục Oy.

Ví dụ. Cho điểm M(2 ; 4). Tìm ảnh của điểm M qua phép đối xứng qua trục Ox và trục Oy.

Lời giải:

Gọi ĐOx(M) = A(x ; y) và ĐOy(M) = B(a; b)

Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:

x  = 2y=  −4  ⇒ A(2  ;  −4)

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:

a  = −2b=  4  ⇒ B(−2  ; 4)

7. Tính chất của phép đối xứng trục

– Tính chất 1. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

– Tính chất 2. Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

Ví dụ. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Ox, đường tròn (C)

(x – 2)2 + (y – 3)2 = 36 biến thành đường tròn (C’). Tìm phương trình đường tròn (C’) ?

Lời giải:

Đường tròn (C) có tâm I(2 ; 3) và bán kính là R = 6.

Qua phép đối xứng trục Ox, biến đường tròn (C) thành đường tròn (C’), biến tâm I thành tâm I’(x’; y’) và bán kính R’ = R = 6.

Áp dụng biểu thức phép đối xứng trục Ox ta được I’(2; – 3)

Do đó, phương trình đường tròn (C’) là:

(x – 2)2 + (y + 3)2 = 36.

8. Trục đối xứng của một hình

– Định nghĩa. Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu phép đối xứng qua đường thẳng d biến ℋ thành chính nó.

Khi đó, ta nói ℋ là hình có trục đối xứng.

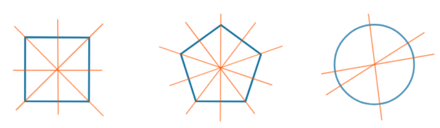
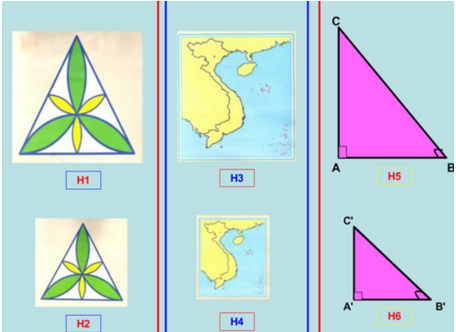
– Ví dụ 3. Các hình sau có trục đối xứng

9. Định nghĩa của phép đối xứng tâm

– Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác điểm I thành điểm M’ sao cho I là trung điểm của đoạn thẳng MM’ được gọi là phép đối xứng tâm I.

Điểm I được gọi là tâm đối xứng.

Phép đối xứng tâm I thường được kí hiệu là ĐI.

– Nếu hình ℋ ‘ là ảnh của hình ℋ  qua ĐI thì ta còn nói ℋ  đối xứng với ℋ ‘ qua tâm I, hay ℋ  và ℋ ‘ đối xứng với nhau qua I.

Từ định nghĩa trên ta suy ra, M’ = ĐI(M) ⇔IM’→  =  − IM→.

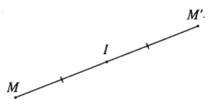
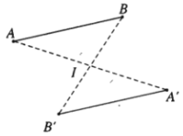
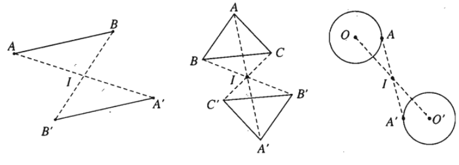
– Ví dụ 1. Cho hình vẽ sau. Các điểm A và B là ảnh của điểm A’ và B’ qua phép đối xứng tâm I và ngược lại.

10. Biểu thức tọa độ của phép đối xứng qua gốc tọa độ

Trong hệ tọa độ Oxy, cho M(x ; y), M’= ĐO(M) = (x’; y’). Khi đó:

 x’  =−xy’ = −y, đây là biểu thức tọa độ của phép đối xứng qua gốc tọa độ.

– Ví dụ. Trong mặt phẳng tọa độ Oxy cho điểm A(7 ; – 4). Tìm ảnh của điểm A qua phép đối xứng tâm O. 

Lời giải:

Gọi A’(x’; y’) là ảnh của điểm A qua  phép đối xứng tâm O. 

Áp dụng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có:

x’  =−7y’ = −(−4)  =  4  ⇒ A’ (−7  ;  4)

11. Tính chất của phép đối xứng tâm

– Tính chất 1. Nếu ĐI(M) = M’ và ĐI(N) = N’ thì M’N’→  =  − MN→, từ đó suy ra M’N’ = MN.

Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì.

– Tính chất 2. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

– Ví dụ. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + y – 2 = 0. Tìm ảnh của d qua phép đối xứng tâm I(1; 2).

Lời giải:

Giả sử phép đối xứng tâm I(1 ; 2) biến điểm  thành điểm M’(x’ ; y’).

Khi đó I là trung điểm của MM’. Áp dụng công thức tọa độ trung điểm ta có:

x’=2.1−x=2−xy’=2.2−y=4−y⇔x=2−x’y=4−y’

Vì điểm M thuộc d nên: x + y – 2 = 0    (2).

Thay (1) vào (2) ta được:

(2 – x’) + (4 – y’) – 2 = 0 hay – x’ – y’ + 4 = 0.

Do đó, phương trình đường thẳng d’ là – x – y + 4 = 0 hay x + y – 4 =0.

12. Tâm đối xứng của một hình

Định nghĩa. Điểm I được gọi là tâm đối xứng của hình ℋ nếu phép đối xứng tâm I biến hình ℋ  thành chính nó.

– Khi đó, ta nói ℋ  là hình có tâm đối xứng.

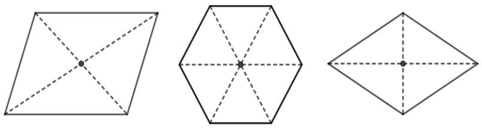
– Ví dụ 4. Các hình sau đây đều có tâm đối xứng:

13. Định nghĩa của phép quay

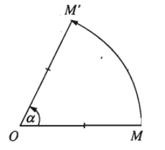
– Định nghĩa: Cho điểm O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc α.

– Điểm O được gọi là tâm quay, α được gọi là góc quay của phép quay đó.

Phép quay tâm O góc α được kí hiệu là Q(O, α).

– Nhận xét:

1) Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều ngược với chiều quay của kim đồng hồ.

2) Với k là số nguyên ta luôn có:

Phép quay Q(O,  k2π) là phép đồng nhất.

Phép quay Q(O, (2k​+1)π) là phép đối xứng tâm O.

14. Tính chất của phép quay

– Tính chất 1. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.

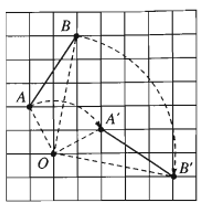
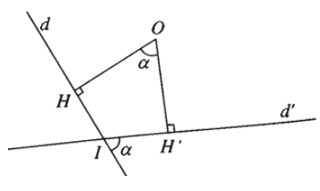
Phép quay tâm O, góc (OA, OA’) biến điểm A thành A’, B thành B’. Khi đó ta có A’B’ = AB.

– Tính chất 2. Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

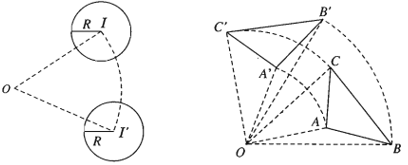
– Nhận xét: Phép quay góc α với , biến đường thẳng d thành đường thẳng d’ sao cho góc giữa d và d’ bằng α (nếu 0  <  α ≤π2), hoặc bằng π-α (nếu  π2  ≤  α  < π)

15. Khái niệm về phép dời hình

– Định nghĩa: Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.

Nếu phép dời hình F biến các điểm M, N lần lượt thành các điểm M’; N’ thì

MN = M’N’.

– Nhận xét:

1) Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép dời hình.

2) Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép dời hình.

– Ví dụ 1. Vì phép tịnh tiến và phép đối xứng tâm là phép dời hình nên thực hiện liên tiếp phép tịnh tiến theo vectơ  và phép đối xứng tâm O ta được một phép dời hình.

16. Tính chất của phép dời hình

Phép dời hình:

1) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.

2) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.

3) Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.

4) Biến đường tròn thành đường tròn có cùng bán kính.

– Chú ý:

a) Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

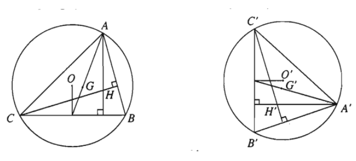
b) Phép dời hình biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thành đỉnh, biến cạnh thành cạnh.

– Ví dụ . Cho đường tròn (C) có phương trình (x + 4)2 + (y – 3)2 = 49. Thực hiện liên tiếp phép đối xứng trục qua đường thẳng d và phép quay tâm O góc quay 900 ta được đường tròn (C’).

Bán kính đường tròn (C’) là: R’ = R = 7.

17. Khái niệm hai hình bằng nhau

– Định nghĩa. Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

– Ví dụ.

a)  Qua phép tịnh tiến theo vectơ  biến tam giác ABC thành tam giác A’B’C’. Sau đó, ta thực hiện tiếp phép đối xứng trục qua đường thẳng d biến tam giác A’B’C’ thành tam giác A”B”C”. Khi đó: ∆ABC = ∆A”B”C”.

b) Hình ảnh dưới đây cho ta hai hình bằng nhau:

18. Định nghĩa của phép vị tự

– Cho điểm O và số k ≠ 0. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho OM’→  =  k. OM→ được gọi là phép vị tự tâm O, tỉ số k.

Phép vị tự tâm O tỉ số k thường được kí hiệu là V(O, k).

– Nhận xét:

1) Phép vị tự biến tâm vị tự thành chính nó.

2) Khi k = 1, phép vị tự là phép đồng nhất.

3) Khi k = -1, phép vị tự là phép đối xứng qua tâm vị tự.

4) M’ = V(O, k)(M) ⇔M =  VO, 1k (M’).

19. Tính chất của phép vị tự

– Tính chất 1. Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M’, N’ thì M’N’→  =  k.MN→ và M’N’ = |k|.MN.

– Tính chất 2.

Phép vị tự tỉ số k:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

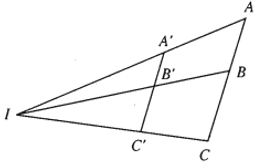
b) Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

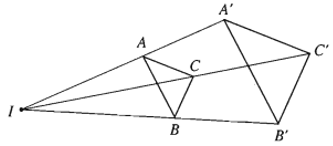
d) Biến đường tròn bán kính R thành đường tròn có bán kính |k|.R.

20. Tâm vị tự của hai đường tròn.

– Định lí: Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.

Tâm của phép vị tự được gọi là tâm vị tự của hai đường tròn.

– Cách tìm tâm vị tự của hai đường tròn.

Cho hai đường tròn (I ; R) và (I’; R’) có ba trường hợp xảy ra:

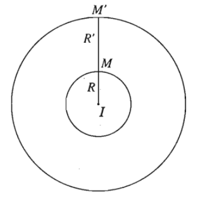
+ Trường hợp I trùng với I’

Khi đó, phép vị tự tâm I tỉ số R’R và phép vị tự tâm I tỉ số -R’R biến đường tròn

(I ; R) thành đường tròn (I ; R’).

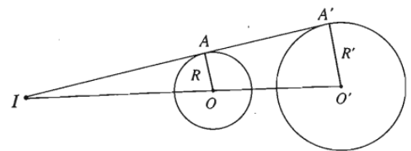
+ Trường hợp I khác I’ và R ≠ R’

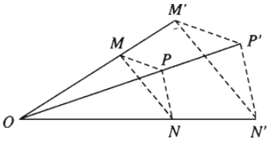
Lấy điểm M bất kì thuộc đường tròn (I ; R), đường thẳng qua I’ song song với IM cắt đường tròn (I’ ; R’) tại M’ và M”.

Giả sử M, M’ nằm cùng phía đối với đường thẳng II’ còn M, M” nằm khác phía đối với đường thẳng II’.

Giả sử đường thẳng MM’ cắt đường thẳng II’ tại điểm O nằm ngoài đoạn thẳng II’, còn đường thẳng MM” cắt đường thẳng II’ tại điểm O1 nằm trong đoạn thẳng II’.

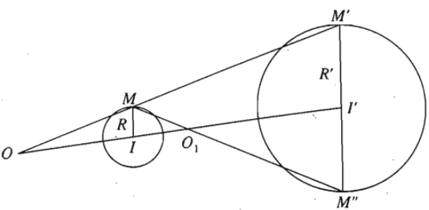
Khi đó, phép vị tự tâm O tỉ số k  =  R’R và phép vị tự tâm O1 tỉ số k1 =  −R’R sẽ biến đường tròn (I ; R) thành đường tròn (I’; R’).

Ta gọi O là tâm vị tự ngoài còn O1 là tâm vị tự trong của hai đường tròn nói trên.

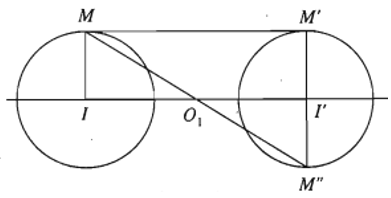
+ Trường hợp I khác I’ và R = R’.

Khi đó, MM’ // II’ nên chỉ có phép vi tự tâm O1 tỉ số k  =  −RR  =  −1 biến đường tròn (I; R) thành đường tròn (I’ ; R’). Đây chính là phép đối xứng tâm O1.

Ví dụ 1. Cho hai đường tròn (C): (x – 2)2 + (y – 1)2 = 4 và (C’): (x – 8)2 + (y – 4)2 = 16. Xác định tâm vị tự của hai đường tròn?

Lời giải:

Đường tròn (C) có tâm I(2 ; 1),bán kính R = 1;

Đường tròn (C’) có tâm I’(8 ; 4), bán kính R’ = 4.

Do I  ≠  I’ và R ≠ R’ nên có hai phép vị tự V(J, 2) và V(J, -2) biến (C) thành (C’).

Gọi J(x ; y)

Với k = 2 khi đó:

JI’→=2JI→⇔8−x=22−x4−y=21−y⇔x=−4y=−2

Suy ra: J(– 4; – 2)

Tương tự với k = – 2, tính có J’(4; 2).

Vậy có 2 phép vị tự thỏa mãn đầu bài.

21. Định nghĩa phép đồng dạng

– Định nghĩa: Phép biến hình F được gọi là phép đồng dạng tỉ số k (k > 0), nếu với hai điểm M, N bất kì và ảnh M’, N’ tương ứng của chúng ta luôn có M’N’ = kMN.

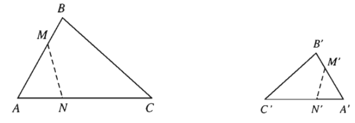
– Nhận xét

(1) Phép dời hình là phép đồng dạng tỉ số 1.

(2) Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

22. Tính chất phép đồng dạng

Phép đồng dạng tỉ số k:

a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.

d) Biến đường tròn bán kính R thành đường tròn có bán kính kR.

– Chú ý.

a) Nếu một phép đồng dạng biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

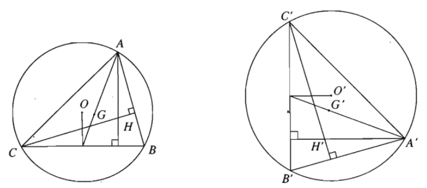
b) Phép đồng dạng biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thảng đỉnh, biến cạnh thành cạnh.

Ví dụ. Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 đường tròn (C) và (C’) có phương trình x2 + y2 – 4y – 5 = 0 và x2 + y2 – 2x + 2y – 14 = 0. Gọi (C’) là ảnh của (C) qua phép đồng dạng tỉ số k, khi đó giá trị k là ?

Lời giải:

Đường tròn (C) có tâm I(0 ; 2) bán kính R = 3.

Đường tròn (C’) có tâm I’(1 ; – 1) bán kính R’ = 4.

Ta có (C’) là ảnh của (C) qua phép đồng dạng tỉ số k nên : 4 = 3k

Suy ra : k  =  43 .

Vậy k  =  43.

23. Hình đồng dạng

– Định nghĩa. Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.

– Ví dụ. Các hình sau đôi một đồng dạng với nhau.

Xem thêm:

Đề thi giữa học kì 1 Toán lớp 11 Trắc nghiệm + Tự luận năm 2022 – 2023 

Phòng Giáo dục và Đào tạo …..

Đề khảo sát chất lượng giữa học kì 1

Năm học 2022 – 2023

Môn: Toán 11

Thời gian làm bài: 45 phút

(Đề số 1)

I. Trắc nghiệm

Câu 1. Tập xác định của hàm số y=cotxcosx−1 là

A. ℝ\kπ2,k∈Z

B. ℝ\π2+kπ,k∈Z

C. ℝ\kπ,k∈Z

D. ℝ

Câu 2. Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1). Hỏi điểm nào sau đây là ảnh của điểm M qua phép quay tâm O(0; 0), góc quay 45o?

A. M’0;2

B. M’2;0

C. M’0;1

D. M’1;−1

Câu 3. Hàm số y = sin2x đồng biến trên khoảng nào trong các khoảng sau?

A. 0;π4

B. π2;π

C. π;3π2

D. 3π2;2π

Câu 4. Gọi d’ là hình ảnh của d qua tâm I góc quay φ (biết I không nằm trên d ), đường thẳng d’ song với d khi:

A. φ=π3

B. φ=π6

C. φ=2π3

D. φ=−π

Câu 5. Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y=−sinx

B. y=cosx−sinx

C. y=cosx+sin2x

D. y=cosxsinx

Câu 6. Trong mặt phẳng tọa độ Õxy, cho đường tròn C: x2+y2+6x+5=0. Tìm ảnh đường tròn (C’) của (C) qua QO,900.

A. x2+y−32=4

B. C: x2+y2+6y−6=0

C. x2+y+32=4

D. C: x2+y2+6x−5=0

Câu 7. Một tổ học sinh có 5 nam và 5 nữ xếp thành một hàng dọc thì số các cách xếp khác nhau là:

A. 25

B. 10

C. 10!

D. 40

Câu 8. Cho hình vuông ABCD tâm I . Gọ M, N lần lượt là trung điểm AD, DC. Phép tịnh tiến theo vectơ nào sau đây biến tam giác AMI thành INC.

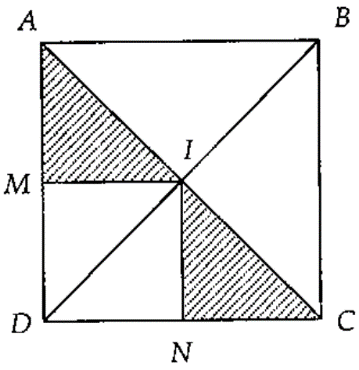
A. AM→

B. IN→

C. AC→

D. MN→

Câu 9. Tìm chu kì T của hàm số y=2sin2x+3cos23x

A. T=π

B. T=2π

C. T=3π

D. T=π3

Câu 10. Có 5 học sinh nam và 3 học sinh nữ xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp để 2 học sinh nam xen giữa 3 học sinh nữ? (đổi 2 học sinh bất kì được cách mới)

A. 2880

B. 5760

C. 1440

D. 4320

Câu 11. Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d:2x−3y+3=0 và d’:2x−3y−5=0. Tìm tọa độ v→ có phương vuông góc với d và Tv→ biến đường thẳng d thành d’

A. v→=−613;413

B. v→=−113;213

C. v→=−1613;−2413

D. v→=1613;−2413

Câu 12. Gọi M; m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=8sin2x+3cos2x. Tính P=2M−m2.

A. 1

B. 2

C. 112

D. 130

Câu 13. Nếu bốn số hạng đầu của một hàng trong tam giác Pascal được ghi lại là:     1        16      120    560

Khi đó 4 số hạng đầu của hàng kế tiếp là:

A. 1         32         360         1680

B. 1         18         123         564

C. 1         17         137         697

D. 1         17         136         680

Câu 14. Có 3 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?

A. 200

B. 30

C. 300

D. 120

Câu 15. Hình gồm hai đường thẳng d và d’ vuông góc với nhau đó có mấy trục đối xứng?

A. 0

B. 2

C. 4

D. Vô số

Câu 16. Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O, góc quay α≠k2π, k∈ℤ.

A. Không có.

B. Một.

C. Hai.

D. Vô số.

Câu 17. Với giá trị nào của x thì giá trị của các hàm số y=sin3x và y=sinx bằng nhau?

A. x=k2πx=π4+k2πk∈Z.

B. x=kπx=π4+kπ2k∈Z.

C. x=kπ4 k∈Z.

D. x=kπ2 k∈Z.

Câu 18. Nghiệm của phương trình sinx.2cosx−3=0 là:

A. x=kπx=±π6+k2π, k∈ℤ

B. x=kπx=±π6+kπ, k∈ℤ

C. x=k2πx=±π3+k2π, k∈ℤ

D. x=±π6+k2π, k∈ℤ

Câu 19. Trong mặt phẳng Oxy, cho điểm M2;3. Hỏi M là ảnh của điểm nào trong các điểm sau qua phép đối xứng trục Oy?

A. 3;2

B. 2;–3

C. 3;–2

D. –2;3

Câu 20. Từ A đến B có 3 con đường, từ B đến C có 4 con đường. Hỏi có bao nhiêu cách chọn đường từ A đến C (qua B) và trở về C đến A (qua B) và không đi lại các con đường đã đi rồi?

A. 72

B. 132

C. 18

D. 23

Câu 21. Giải phương trình 8cot2x=cos2x−sin2x.sin2xcos6x+sin6x

A. x=−π4+kπ

B. x=±π4+kπ2

C. x=π4+kπ

D. x=π4+kπ2

Câu 22. Nghiệm của phương trình lượng giác: 2sin2x-3sinx+1=0 điều kiện 0≤x<π2 là:

A. x=π3

B. x=π2

C. x=π6

D. x=5π6

Câu 23. Có bao nhiêu số tự nhiên gồm lẻ gồm 4 chữ số khác nhau? Đáp số của bài toán là

A. 2420

B. 3208

C. 2650

D. Kết quả khác

Câu 24. Tìm số tự nhiên n thỏa mãn An3 = 20n

A. n = 5

B. n = 6

C. n = 10

D. n = 12

Câu 25. Tìm số hạng không chứa x trong khai triển của

A. 126720

B. –126720

C. 7920

D. –7920

II. Tự luận

Câu 1. Giải phương trình lượng giác cotx−1=cos2x1+tanx+sin2x−12sin2x

Câu 2. Có 5 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy?

Phòng Giáo dục và Đào tạo …..

Đề khảo sát chất lượng giữa học kì 1

Năm học 2022 – 2023

Môn: Toán 11

Thời gian làm bài: 45 phút

(Đề số 2)

I. Trắc nghiệm

Câu 1. Tập xác định của hàm số y=3sin2x−cos2x là

A. ℝ\π4+kπ,k∈Z

B. ℝ\π2+kπ,k∈Z

C. ℝ\π4+kπ2,k∈Z

D. ℝ\3π4+k2π,k∈Z

Câu 2. Trong khai triển nhị thức 1+x6 xét các khẳng định sau:

I. Gồm có 7 số hạng.

II. Số hạng thứ 2 là 6x.

III. Hệ số của x5 là 5.

Trong các khẳng định trên

A. Chỉ I và III đúng

B. Chỉ II và III đúng

C. Chỉ I và II đúng

D. Cả ba đúng

Câu 3. Cho hai đường thẳng d1 và d2 cắt nhau. Có bao nhiêu phép tịnh tiến biến d1 thành d2

A. Không.

B. Một.

C. Hai.

D. Vô số.

Câu 4. Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc α biến hình vuông thành chính nó ?

A. 1

B. 2

C. 3

D. 4

Câu 5. Với x∈0;π4, mệnh đề nào sau đây là đúng?

A. Cả hai hàm số y=−sin2x và y=−1+cos2x đều nghịch biến.

B. Cả hai hàm số y=−sin2x và y=−1+cos2x đều đồng biến.

C. Hàm số y=−sin2x nghịch biến, hàm số y=−1+cos2x đồng biến.

D. Hàm số y=−sin2x đồng biến, hàm số y=−1+cos2x nghịch biến.

Câu 6. Cho các chữ số 0; 1; 2; 4; 5; 6; 8. Hỏi từ các chữ số trên lập được tất cả bao nhiêu số có 5 chữ số khác nhau chia hết cho 5 mà trong mỗi số chữ số 1 luôn xuất hiện?

A. 444

B. 480

C. 420

D. 468

Câu 7. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình 5x−3y+15−0. Tìm ảnh d’ của d qua phép quay QO,900 với O là gốc tọa độ?

A. 5x−3y+6=0

B. 3x+5y+15=0

C. 5x+y−7=0

D. −3x+5y+7=0

Câu 8. Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y=sinx

B. y=x2.sinx

C. y=xcosx

D. y=x+sinx

Câu 9. Trong mặt phẳng tọa độ Oxy, viết phương trình đường tròn (C’) là ảnh của C:x2+y2−2x+4y−4=0 qua phép quay QO,−π2.

A. x+22+y+12=9

B. x−22+y−12=9.

C. x−232+y+12=9.

D. x−12+y+22=9.

Câu 10. Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. y=xcosx

B. y=xtanx

C. y=tanx

D. y=1x

Câu 11. Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau?

A. 120

B. 60

C. 30

D. 40

Câu 12. Trong mặt phẳng tọa độ , cho hình bình hành OABC với điểm A−2;1, điểm B thuộc đường thẳng Δ:2x−y−5=0. Tìm quỹ tích đỉnh C?

A. Là đường thẳng có phương trình  2x−y−10=0

B. Là đường thẳng có phương trình x+2y−7=0

C. Là đường thẳng có phương trình 2x−y+7=0

D. Là đường tròn có phương trình x2+y2−2x+y=0

Câu 13. Tìm chu kì T của hàm số y=cos2x+sinx2

A. T=4π

B. T=π

C. T=2π

D. T=π2

Câu 14. Giả sử một công việc có thể được tiến hành theo hai phương án A và B. Phương án A có thể thực hiện bằng n cách, phương án B có thể thực hiện bằng m cách không trùng với cách nào của phương án A. Khi đó:

A. Công việc có thể được thực hiện bằng m.n cách.

B. Công việc có thể được thực hiện bằng 12n.m cách.

C. Công việc có thể được thực hiện bằng m + n cách.

D. Công việc có thể thực hiện bằng 12(m+n) cách.

Câu 15. Cho tam giác đều ABC có tâm O. Phép quay tâm O, góc quay φ biến tam giác đều thành chính nó thì góc quay φ là góc nào sau đây:

A. π3

B. 2π3

C. 3π2

D. π2

Câu 16. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=sin2x+2cos2x

A. M=3, m=0

B. M=2, m=0

C. M=2, m=1

D. M=3, m=1

Câu 17. Trong mặt phẳng Oxy. Phép đối xứng tâm O(0; 0) biến điểm M(-2; 3)  thành điểm:

A. M’ (-4; 2)

B. M’ (2; -3)

C. M'(-2; 3)

D. M’ (2; 3)

Câu 18. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình tanx = 1?

A. sinx=22

B. cosx=22

C. cotx=1

D. cot2x=1

Câu 19. Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?

A. Không có.

B. Một.

C. Hai. 

D. Vô số

Câu 20. Nghiệm của pt 3.cos2x = – 8.cosx – 5 là:

A. x=kπ

B. x=π+k2π

C. x=k2π

D. x=±π2+k2π

II. Tự luận

Câu 1. Có 5 học sinh nam và 3 học sinh nữ xếp thành một hàng dọc. Hỏi có bao nhiêu cách xếp để 2 học sinh nam xen giữa 3 học sinh nữ? (đổi 2 học sinh bất kì được cách mới)

Câu 2.Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo véctơ v→=(a;b) biến đường thẳng d1:x+y=0 thành d1′:x+y−4=0 và d2:x−y+2 thành d2′:x−y−8=0. Tính m=a+b.

Câu 3. Tìm tất cả giá trị của m để phương trình sin2x-2(m-1)sinxcosx-(m-1)cos2x=m có nghiệm?

Phòng Giáo dục và Đào tạo …..

Đề khảo sát chất lượng giữa học kì 1

Năm học 2022 – 2023

Môn: Toán 11

Thời gian làm bài: 45 phút

(Đề số 3)

Câu 1. Tập xác định của hàm số y=1−3cosxsinxlà

A. x≠π2+kπ

B. x≠k2π

C. x≠kπ2

D. x≠kπ

Câu 2. Cho A=a; b; c. Số hoán vị của ba phần tử của A là:

A. 4

B. 5

C. 6

D. 7

Câu 3. Kết luận nào sau đây là sai?

A. Tu→(A)=B⇔AB→=u→

B. TAB→(A)=B

C. T0→(B)=B

D. T2AB→(M)=N⇔AB→=2MN→

Câu 4. Trong các mệnh đề sau mệnh đề nào đúng?

A. Phép đối xứng trục không có điểm nào biến thành chính nó.

B. Phép đối xứng trục có đúng một điểm biến thành chính nó.

C. Có phép đối xứng trục có hai điểm biến thành chính nó.

D. Có phép đối xứng trục có vô số điểm biến thành chính nó

Câu 5. Hàm số nào đồng biến trên khoảng −π3;π6

A. y=cosx

B. y=cot2x

C. y=sinx

D. y=cos2x

Câu 6. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tạo độ?

A. y=cot4x

B. y=sinx+1cosx

C. y=tan2x

D. y=cotx

Câu 7. Cho tập A=1;2;3;4;5;6;7;8;9. Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau sao cho số đó không bắt đầu bởi 125?

A. 265

B. 262

C. 6072

D. 6705

Câu 8. Trong mặt phẳng tọa độ Oxy, tìm phương trình đường thẳng Δ’ là ảnh của đường thẳng Δ:x+2y−1=0 qua phép tịnh tiến theo véctơ v→=1;−1.

A.  Δ’:x+2y=0

B. Δ’:x+2y−3=0

C. Δ’:x+2y+1=0

D. Δ’:x+2y+2=0

Câu 9. Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?

A. y=sinx

B. y=x+1

C. y=x2

D. y=x−1x+2

Câu 10. Trong mặt phẳng Oxy, cho điểm M(3; 4). Tìm toạ độ điểm N sao cho điểm M  là ảnh của N qua phép quay tâm I2; 3, góc quay 90∘.

A. (3; 2)

B. (2; 3)

C. (1; 3)

D. (3; -2)

Câu 11. Từ tỉnh A tới tỉnh B có thể đi bằng ô tô, tàu hỏa, tàu thủy hoặc máy bay. Từ tỉnh B tới tỉnh C có thể đi bằng ô tô hoặc tàu hỏa. Muốn đi từ tỉnh A đến tỉnh C bắt buộc phải đi qua B. Số cách đi từ tỉnh A đến tỉnh C là:

A. 4

B. 2

C. 6

D. 8

Câu 12: Tìm chu kì T của hàm số y=3cos2x+1−2sinx2−3

A. T=2π

B. T=4π

C. T=6π

D. T=π

Câu 13. Trong khai triển (1+30)20 với số mũ tăng dần, hệ số của số hạng đứng chính giữa là:

A. 39C209

B. 312C2012

C. 311C2011

D. 310C2010

Câu 14. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số .

A. M=3, m=−1

B. M=1, m=−1

C. M=2, m=−2

D. M=0, m=−2

Câu 15. Nghiêm của pt 3.cos2x = – 8.cosx – 5  là:

A. x=kπ

B. x=π+k2π

C. x=k2π

D. x=±π2+k2π

Câu 16. Có bao nhiêu giá trị nguyên của m để phương trình 2sinx+mcosx=1−m  (1) có nghiệm x∈−π2;π2.

A. 5

B. 4

C. 6

D. 3

Câu 17. Nghiệm của phương trình tan2x+100+cotx=0 là:

A. x=−1000+k1800

B. x=1000+k1800

C. x=−100+k1800

D. x=100+k1800

Câu 18. Có 8 nhà khoa học Toán (6 nam, 2 nữ) và 5 nhà khoa học Vật Lí (toàn nam). Hỏi có bao nhiêu cách lập một đội gồm 4 nhà khoa học trong đó có cả nam, nữ, cả Toán, Vật Lí?

A. 270

B. 300

C. 375

D. 570

Câu 19. Trong mặt phẳng tọa độ Oxy, cho điểm A0;3. Tìm tọa độ điểm A’ là ảnh của A qua phép quay QO,−450.

A. A’12;32

B. A’34;14

C. A’−32;12

D. A’32;32

Câu 20. Trong mặt phẳng tọa độ Oxy cho điểm A(2; 5). Hỏi A là ảnh của điểm nào trong các điểm sau qua phép tịnh tiến theo vectơ v→=(1; 2)?

A. (1;3)

B. (1; 6)

C. ( 3; 7)

D. ( 2; 4)

II. Tự luận

Câu 1. Giải phương trình cosx(cosx+2sinx)+3sinx(sinx+2)sin2x-1=1

Câu 2. Từ 5 chữ số 1, 2, 3 có thể lập được bao nhiêu số các số gồm 7 chữ số, trong đó chữ số 1 có mặt 3 lần, chữ số 2 có mặt đúng 2 lần, chữ số 3 có mặt 2 lần.

Câu 3. Trong mặt phẳng tọa độ Oxy, cho A1; 2; B4; 4. Tìm điểm M thuộc Ox sao cho MA + MB nhỏ nhất?

Xem thêm các bộ đề thi Toán lớp 11 chọn lọc, hay khác:

TOP 30 Đề thi Học kì 1 Toán lớp 11 năm 2022 – 2023 có đáp án

Đề cương Học kì 1 Toán lớp 11 năm 2022 – 2023 chi tiết nhất

Bài tập Toán lớp 11 Học kì 1 có đáp án

Các dạng bài tập Toán lớp 11 Học kì 1

Hệ thống kiến thức Toán lớp 11 Học kì 1