Đề cương ôn tập học kì 1 toán 9 – loigiaihay.com
Lựa chọn câu để xem lời giải nhanh hơn
LT đại số
I. CĂN BẬC HAI CĂN BẬC BA
1) Định nghĩa, tính chất căn bậc hai
a) Với số dương a, số \(\sqrt a \) được gọi là căn bậc hai số học của a.
b) Với a ≠ 0 ta có x =\(\sqrt a \) <=> \(\left\{ \begin{array}{l}x{\rm{ }} \ge {\rm{ }}0\\{x^2} = {\left( {\sqrt a } \right)^2} = {\rm{ }}a\end{array} \right.\)
c) Với hai số a và b không âm, ta có: a < b <=> \(\sqrt a < \sqrt b \)
d) \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}{\rm{A , A}} \ge {\rm{0}}\\ – A,{\rm{ A }} < {\rm{ 0}}\end{array} \right.\)
2) Các công thức biến đổi căn thức
1. \(\sqrt {{{\rm{A}}^{\rm{2}}}} = \left| {\rm{A}} \right|\)
2. \(\sqrt {{\rm{AB}}} = \sqrt {\rm{A}} .\sqrt {\rm{B}} \) (\(A \ge 0\), \(B \ge 0\))
3. \(\sqrt {\frac{A}{B}} = \frac{{\sqrt A }}{{\sqrt B }}\) (\(A \ge 0\), B > 0)
4. \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \) (\(A \ge 0\))
5. \(A\sqrt B = \sqrt {{A^2}B} \) (\(A \ge 0\), \(B \ge 0\)) \(A\sqrt B = – \sqrt {{A^2}B} \) (A < 0,\(B \ge 0\))
6. \(\sqrt {\frac{A}{B}} = \frac{1}{{\left| B \right|}}\sqrt {AB} \) (\(AB \ge 0\), \(B ≠ 0\))
7. \(\frac{C}{{\sqrt A \pm B}} = \frac{{C\left( {\sqrt A \mp B} \right)}}{{A – {B^2}}}\) (\(A \ge 0\), A ≠ B2)
8. \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\) (B > 0)
9.\(\frac{C}{{\sqrt A \pm \sqrt B }} = \frac{{C\left( {\sqrt A \mp {\rm{ }}\sqrt B } \right)}}{{A – B}}\)(\(A,B \ge 0\, ,A ≠ B\))
Các bước thực hiện bài toán rút gọn:
1.Tìm ĐKXĐ của biểu thức: là tìm TXĐ của từng phân thức rồi kết luận lại.
2. Phân tích tử và mẫu thành nhân tử (rồi rút gọn nếu được)
3. Quy đồng, gồm các bước:
+ Chọn mẫu chung: là tích các nhân tử chung và riêng, mỗi nhân tử lấy số mũ lớn nhất.
+ Tìm nhân tử phụ: lấy mẫu chung chia cho từng mẫu để được nhân tử phụ tương ứng.
+ Nhân nhân tử phụ với tử – Giữ nguyên mẫu chung.
4. Bỏ ngoặc: bằng cách nhân đa thức hoặc dùng hằng đẳng thức.
5.Thu gọn: là cộng trừ các hạng tử đồng dạng.
6. Phân tích tử thành nhân tử ( mẫu giữ nguyên).
7. Rút gọn.
II. HÀM SỐ
Khái niệm hàm số
* Nếu đại lượng y phụ thuộc vào đại lượng x sao cho mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x được gọi là biến số.
* Hàm số có thể cho bởi công thức hoặc cho bởi bảng.
II. HÀM SỐ BẬC NHẤT:
Kiến thức cơ bản:
1) Định nghĩa, tính chất hàm số bậc nhất
a) Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b (a, b thuộc R và a ≠ 0)
b) Hàm số bậc nhất xác định với mọi giá trị x thuộc R.
Hàm số đồng biến trên R khi a > 0. Nghịch biến trên R khi a < 0.
2) Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b (a: hệ số góc, b: tung độ gốc).
3) Cho (d): y = ax + b và (d’): y = a’x + b’ (a, a’ ≠ 0). Ta có:
(d) trùng (d’) \( \Leftrightarrow \left\{ \begin{array}{l}a = a’\\b = b’\end{array} \right.\)
(d) song song (d’)\({\rm{ }} \Leftrightarrow {\rm{ }}\left\{ \begin{array}{l}a = a’\\b \ne b’\end{array} \right.\)
(d) cắt (d’) <=> a ≠ a’
(d) vuông góc (d’) \({\rm{ }} \Leftrightarrow {\rm{ }}a.a'{\rm{ }} = {\rm{ }} – 1\)
4) Gọi a là góc tạo bởi đường thẳng y = ax + b và trục Ox thì:
Khi a > 0 ta có tana = a
Khi a < 0 ta có tana’\( = \left| a \right|\) (a’ là góc kề bù với góc a)
LT hình học
I/ HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
1./ AB2 = BH.BC ; AC2 = CH. BC
2/ AB2 +AC2 = BC2
3/ AH2 = HB. HC
4/ AH .BC = AB . AC
5/ \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
II/ TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN TRONG TAM GIÁC VUÔNG
sin C =\(\frac{{AB}}{{BC}}\); cos C =\(\frac{{AC}}{{BC}}\) ;
tanC =\(\frac{{AB}}{{AC}}\); cotC =\(\frac{{CA}}{{BA}}\)
sin B = cosC; sin C = cosB; tan B = cotC; tan C = cotB
Trong một tam giác vuông
* Hai góc phụ nhau thì sin góc này bằng cos góc kia hoặc tan góc này bằng cot góc kia.
* Cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề.
* Cạnh góc vuông này bằng cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề.
III/ ĐƯỜNG TRÒN
Nội Dung Chính
Đường kính và dây cung của đường tròn
– Trong các dây của đường tròn, đường kính là dây lớn nhất
– Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây đó
– Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây đó.
Liên hệ giữa dây và khoảng cách đến tâm
– Trong một đường tròn:
a. Hai dây bằng nhau thì cách đều tâm
b. Hai dây cách đều tâm thì bằng nhau
– Trong hai dây của một đường tròn
a. Dây nào lớn hơn thì dây đó gần tâm hơn
b. Dây nào gần tâm hơn thì dây đó lớn hơn
Vị trí tương đối của hai đường tròn
1. Cho đường thẳng a và đường tròn (O ; R), gọi d là khoảng cách từ O đến a
d > R <=> a và (O) không giao nhau
d = R <=> a và (O) tiếp xúc nhau (có 1 điểm chung)
d < R <=> a và (O) cắt nhau (có 2 điểm chung)
Tính chất hai tiếp tuyến cắt nhau
– ĐN: Tiếp tuyến của đường tròn là đường thẳng chỉ có một điểm chung với đường tròn đó.
– T/C: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
– Dấu hiệu: Nếu một đường thẳng đi qua một tiếp điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của một đường tròn.
– Tính chất hai tiếp tuyến cắt nhau tại một điểm
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại 1 điểm thì:
- Điểm đó cách đều hai tiếp điểm
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm
BT trắc nghiệm
Câu 1. Căn bậc hai số học của số a không âm là:
A. Số có bình phương bằng a B.\(\sqrt a \)
C. -\(\sqrt a \) D. B,C đều đúng
Câu 2. Hàm số y= (m-1)x –3 đồng biến khi:
A. m >1 B.m
C. m\( \ge \)1 D. Một kết quả khác
Câu 3. Cho x là một góc nhọn , trong các đẳng thức sau đẳng thức nào đúng:
A.Sinx+Cosx=1 B.Sinx=Cos(900-x)
C. Tanx=Tan(900-x) D. A,B,C đều đúng
Câu 4. Cho hai đường tròn (O;4cm) , (O’;3cm) và OO’= 5cm. Khi đó vị trí tương đối của (O) và (O’) là:
A. Không giao nhau B. Tiếp xúc ngoài
C. Tiếp xúc trong D. Cắt nhau
Câu 5: Điều kiện của biểu thức \(\sqrt {\frac{1}{{ – 2x + 5}}} \) có nghĩa là:
A. \(x < \frac{5}{2}\) B. \(x > \frac{5}{2}\)
C. \(x \ge \frac{5}{2}\) D. \(x \le \frac{5}{2}\)
Câu 6: Giá trị biểu thức \(\sqrt {4 – 2\sqrt 3 } \) là:
A. \(1 – \sqrt 3 \) B. \(\sqrt 3 – 1\)
C. \(\sqrt 3 + 1\) D. Đáp án khác
Câu 7: Hàm số y = ( – 3 – 2m )x – 5 luôn nghịch biến khi:
A. \(m < – \frac{3}{2}\) B. \(m \le – \frac{3}{2}\)
C. \(m > – \frac{3}{2}\) D. Với mọi giá trị của m
Câu 8: Đồ thị hàm số y = ( 2m – 1) x + 3 và y = – 3x + n là hai đường thẳng song song khi:
A. \(m = – 2\) B. \(m = – 1\)
C. \(m = – 1\) và \(n \ne 3\) D. \(m = \frac{1}{2}\) và \(n \ne 3\)
Câu 9: Cho hình vẽ, \(\sin \alpha \) là:
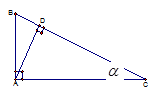
A. \(\sin \alpha = \frac{{AD}}{{AC}}\)
B.\(\sin \alpha = \frac{{BD}}{{AD}}\)
C.\(\sin \alpha = \frac{{BA}}{{AC}}\)
D.\(\sin \alpha = \frac{{AD}}{{BC}}\)
Câu 10: Cho tam giác ABC, góc A = 900,có cạnh AB = 6, \(tgB = \frac{4}{3}\) thì cạnh BC là:
A. 8 B. 4,5 C. 10 D. 7,5
Câu 11: Cho ( O; 12 cm), một dây cung của đường tròn tâm O có độ dài bằng bán kính. Khoảng cách từ tâm đến dây cung là:
A. 6 B. \(6\sqrt 3 \) C.\(6\sqrt 5 \) D. 18
Câu 12: Hai đường tròn ( O; R) và ( O’ ; R’) có OO’ = d. Biết R = 12 cm, R’ = 7 cm, d = 4 cm thì vị trí tương đối của hai đường tròn đó là:
A. Hai đường tròn tiếp xúc nhau. B. Hai đường tròn ngoài nhau.
C. Hai đường tròn cắt nhau D. Hai đường tròn đựng nhau
Câu 13: Biểu thức \(\sqrt {{{( – x)}^2}} \) được xác định khi:
A. mọi x thuộc R B. x\( \le \)0 C. x = 0 D. x\( \ge \)0
Câu 14: Hai đường thẳng y = x + 1 và y = 2x – 2 cắt nhau tại điểm có toạ độ là:
A. ( -3;4 ) B. (1; 2 ) C. ( 3;4) D. (2 ; 3 )
Câu 15: Hệ phương trình \(\left\{ \begin{array}{l}2x + y = 5\\3x – y = 5\end{array} \right.\) có nghiệm là :\(\frac{{1 – x}}{{\sqrt {{x^2} – 2x + 1} }}\)
A. \(\left\{ \begin{array}{l}x = – 2\\y = 1\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = – 2\\y = – 1\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = – 1\\y = – 2\end{array} \right.\)
Câu 16: Điểm (-1 ; 2 ) thuộc đồ thị hàm số nào sau đây:
A. y = 2x + 1 B. y = x – 1 C. y = x + 1 D. y = -x + 1
Câu 17 :Giá trị biểu thức Khi x > 1 là:
A. 1 B. -1 C. 1- x D. \(\frac{1}{{1 – x}}\)
Câu 18: Nếu hai đường tròn có điểm chung thì số tiếp tuyến chung nhiều nhất có thể là:
A. 4 B.3 C.2 D. 1
Câu 19: Tam giác ABC có góc B = 450 ;góc C = 600 ; AC = a thì cạnh AB là:
A. a\(\sqrt 6 \) B. \(\frac{1}{2}a\sqrt 6 \)
C .\(a\sqrt 3 \) D.\(a\sqrt 2 \)
Câu 20: Cho tam giác đều ngoại tiếp đường tròn bán kính 2 cm. Khi đó cạnh của tam giác đều là :
A. \(4\sqrt 3 \) cm B. \(2\sqrt 3 \)cm C. 3cm D. \(3\sqrt 2 \)cm
BT tự luận đại số
Dạng 1: Tìm điều kiện xác định của biểu thức
1) \(\sqrt { – 2x + 3} \) 2) \(\sqrt {\frac{2}{{{x^2}}}} \)
3) \(\sqrt {\frac{4}{{x + 3}}} \) 4) \(\sqrt {\frac{{ – 5}}{{{x^2} + 4}}} \)
5) \(\sqrt {3x + 4} \) 6) \(\sqrt {1 + {x^2}} \)
7) \(\sqrt {\frac{3}{{1 – 2x}}} \) 8)\(\sqrt {\frac{{ – 3}}{{3x + 5}}} \)
Dạng 2: Thực hiện phép tính
1)\(\sqrt {121} – \sqrt {\frac{{25}}{4}} – \sqrt {0,09} \)
2) \(\sqrt {25} + \frac{{\sqrt {49} }}{{\sqrt 4 }} – \sqrt {\frac{9}{4}} – \sqrt {0,16} \)
3) \(2\sqrt {16} – 5\sqrt {{{\left( { – 6} \right)}^2}} – {\left( { – \sqrt 8 } \right)^2}\)
4) \(\sqrt {{{\left( {\sqrt 5 – 2} \right)}^2}} – \sqrt {{{\left( {3 – \sqrt 5 } \right)}^2}} \)
5) \(\sqrt {3 – 2\sqrt 2 } + \sqrt {3 + 2\sqrt 2 } \)
6) \(\sqrt {5 + 2\sqrt 6 } – \sqrt {{{\left( {\sqrt 3 – \sqrt 2 } \right)}^2}} \)
7) \(\sqrt {9 – 4\sqrt 5 } + \sqrt {6 + 2\sqrt 5 } \)
8) \(\sqrt {11 + 2\sqrt {30} } – \sqrt {{{\left( {\sqrt 5 + 2\sqrt 6 } \right)}^2}} \)
9) \(\sqrt {9 – 4\sqrt 2 } – \sqrt {11 + 6\sqrt 2 } \)
10)\(\sqrt {20} – \sqrt {45} + \frac{{\sqrt {15} + \sqrt {10} }}{{\sqrt 3 + \sqrt 2 }}\)
11) \(\left( {\frac{{\sqrt {14} – \sqrt 7 }}{{1 – \sqrt 2 }} + \frac{{\sqrt {15} – \sqrt 5 }}{{1 – \sqrt 3 }}} \right):\frac{1}{{\sqrt 7 – \sqrt 5 }}\)
12) \(6\sqrt {12} – 2\sqrt {48} + 5\sqrt {75} – 7\sqrt {108} \)
13) \(2\sqrt {32} + 3\sqrt {72} – 7\sqrt {50} + \sqrt 2 \)
14) \(\frac{2}{{\sqrt 6 – 2}} + \frac{2}{{\sqrt 6 + 2}} + \frac{5}{{\sqrt 5 }}\)
15) \(\frac{{5 + 2\sqrt 5 }}{{\sqrt 5 }} + \frac{{3 + \sqrt 3 }}{{\sqrt 3 }} – \sqrt 5 – \sqrt 3 \)
16) \(\frac{5}{{\sqrt 6 – 1}} – \frac{{3\sqrt 2 + 2\sqrt 3 }}{{\sqrt 3 + \sqrt 2 }}\)
17)\(\sqrt {{{\left( {2 – \sqrt 7 } \right)}^2}} – \frac{3}{{\sqrt 7 + 2}} + \frac{{2 + \sqrt 2 }}{{\sqrt 2 + 1}}\)
18) \(\left( {1 + \frac{{5 – \sqrt 5 }}{{1 – \sqrt 5 }}} \right)\left( {\frac{{\sqrt 2 – \sqrt {10} }}{{\sqrt 2 }} – 2} \right)\)
19) \(\left( {4 + \sqrt {15} } \right)\left( {\sqrt {10} – \sqrt 6 } \right)\sqrt {4 – \sqrt {15} } \)
20) \(\sqrt {\sqrt 5 – \sqrt {3 – \sqrt {29 – 12\sqrt 5 } } } \)
Dạng 3: Rút gọn biểu thức
Bài 1: Cho biểu thức: \(A = \frac{2}{{\sqrt x – 3}} + \frac{{2\sqrt x }}{{x – 4\sqrt x + 3}} + \frac{{\sqrt x }}{{\sqrt x – 1}}\)
a) Rút gọn A b) Tìm x nếu A = \(\sqrt 3 \)
c) Tìm x thuộc Z để A nhận giá trị nguyên
Bài 2: Cho biểu thức: \(B = \left( {\frac{{2x + 1}}{{\sqrt {{x^3}} – 1}} – \frac{{\sqrt x }}{{x + \sqrt x + 1}}} \right).\left( {\frac{{1 + \sqrt {{x^3}} }}{{1 + \sqrt x }} – \sqrt x } \right)\) Với \(x \ge 0\) và \(x \ne 1\)
a) Rút gọn B b) Tìm x để B = 3
Bài 3: Cho biểu thức: \(C = \left( {\frac{{\sqrt x }}{{3 + \sqrt x }} + \frac{{x + 9}}{{9 – x}}} \right):\left( {\frac{{3\sqrt x + 1}}{{x – 3\sqrt x }} – \frac{1}{{\sqrt x }}} \right)\) Với \(x > 0\) và \(x \ne 9\)
a) Rút gọn C b) Tìm x sao cho \(C < – 1\)
Bài 4: Cho biểu thức: \(D = \frac{1}{{2\sqrt x – 2}} – \frac{1}{{2\sqrt x + 2}} + \frac{{\sqrt x }}{{1 – x}}\)
a) Rút gọn D b) Tính giá trị của D với x = \(\frac{4}{9}\)
c) Tính giá trị của x để \(\left| D \right| = \frac{1}{3}\)
Bài 5: Cho biểu thức : A = \(D = \frac{1}{{2\sqrt x – 2}} – \frac{1}{{2\sqrt x – 2}} + \frac{{\sqrt x }}{{1 – x}}\)với ( x >0 và x ≠ 1)
a) Rút gọn biểu thức A
b) Tính giá trị của biểu thức A tại \(x = 3 + 2\sqrt 2 \)
Bài 6:.Cho biểu thức : \(A = \frac{x}{{\sqrt x – 1}} – \frac{{2x – \sqrt x }}{{x – \sqrt x }}\)với ( x>0 và \(x \ne 1\))
a) Rút gọn biểu thức P; b) Tìm giá trị của a sao cho P = a + 1.
Bài 7: Cho biểu thức \(A = \frac{{x + 1 – 2\sqrt x }}{{\sqrt x – 1}} + \frac{{x + \sqrt x }}{{\sqrt x + 1}}\)
a) Đặt điều kiện để biểu thức A có nghĩa b) Rút gọn biểu thức A
c) Với giá trị nào của x thì A< – 1.
Bài 8: Cho biểu thức: \(G = \,\left( {\frac{{\sqrt x – 2}}{{x – 1}} – \frac{{\sqrt x + 2}}{{x + 2\sqrt x + 1}}} \right).\frac{{{x^2} – 2x + 1}}{2}\)
a) Xác định x để G tồn tại; b) Rút gọn biểu thức G
c) Tính giá trị của G khi x = 0,16; d) Tìm giá trị lớn nhất của G
e) Tìm x thuộc Z để G nhận giá trị nguyên;
f) Chứng minh rằng: Nếu 0 < x < 1 thì M nhận giá trị dương
g) Tìm x để G nhận giá trị âm
Dạng 4: Bài toán về hàm số bậc nhất
Bài 1: Cho hàm số y=2x-1 có đồ thị \(\left( {{d_1}} \right)\) và hàm số y=-x+2 có đồ thị \(\left( {{d_2}} \right)\)
a) Vẽ \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\)trên cùng một mặt phẳng tọa độ Oxy
b) Xác định các hệ số a, b của đường thẳng \(\left( {{d_3}} \right)\): y=ax+b. Biết \(\left( {{d_3}} \right)\)song song với \(\left( {{d_1}} \right)\)và \(\left( {{d_3}} \right)\)đi qua điểm A(2;1)
Bài 2: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng
\(\left( {{d_1}} \right):y = 2x + m,\,\,\left( {{d_2}} \right):y = \left( {{m^2} + 1} \right)x – 1\) (với m là tham số)
1. Tìm m để \(\left( {{d_1}} \right)\) song song với \(\left( {{d_2}} \right)\)
2. Tìm m để \(\left( {{d_1}} \right)\)cắt Ox tại A, cắt Oy tại B(A và B khác O) sao cho \(AB = 2\sqrt 5 \)
3. Tìm tọa độ giao điểm C của \(\left( {{d_1}} \right)\)và \(\left( {{d_2}} \right)\) khi m=2. Xác định a để đường thẳng \(\left( {{d_3}} \right):y = \left( {12 – 5a} \right)x + {a^2} – 2\sqrt {a – 2} \) đi qua điểm C
Bài 3: Cho hàm số bậc nhất: \(y = \left( {k – 2} \right)x + {k^2} – 2k\) (k là tham số)
a) Vẽ đồ thị hàm số khi k=1
b) Tìm k để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2
Bài 4: Cho hàm số bậc nhất: \(y = \left( {m – 1} \right)x + 3\,(1)\,\)(với \(m \ne 1\))
a) Xác định m để hàm số (1) đồng biến trên \(\mathbb{R}\)
b) Xác định m, biết đồ thị của hàm số (1) song song với đường thẳng y=-x+1
c) Xác định m để đường thẳng \(\left( {{d_1}} \right):\,y = 1 – 3x;\,\,\left( {{d_2}} \right):y = – 0,5x – 1,5\)và đồ thị của hàm số (1) cùng đi qua 1 điểm
Bài 5: Cho hai đường thẳng: \(\left( {{d_1}} \right):\,y = 4mx – \left( {m + 5} \right)\) với \(m \ne 0\)
\(\left( {{d_2}} \right):\,y = \left( {3{m^2} + 1} \right) + \left( {{m^2} – 9} \right)\)
a) Với giá trị nào của m thì \(\left( {{d_1}} \right)\)//\(\left( {{d_2}} \right)\)
b) Với giá trị nào của m thì \(\left( {{d_1}} \right)\) cắt \(\left( {{d_2}} \right)\)tìm tọa độ giao điểm khi m=2
c) Chứng minh rằng khi m thay đổi thì đường thẳng \(\left( {{d_1}} \right)\)luôn đi qua điểm cố định A; \(\left( {{d_2}} \right)\)đi qua điểm cố định B. Tính BA
Bài 6: Cho hai đường thẳng: \(\left( {{d_1}} \right):\,y = \frac{1}{2}x + 2\) và \(\left( {{d_2}} \right):\,y = – x + 2\)
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)trên cùng một hệ trục tọa độ Oxy
b) Gọi A và B lần lượt là giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)với trục Ox, C là giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\). Tính chu vi và diện tích của tam giác ABC (đơn vị trên hệ trục tọa độ là cm)?
Bài 7: Cho hàm số y=(m+5)x+2m-10
a) Với giá trị nào của m thì y là hàm số bậc nhất
b) Với giá trị nào của m thì hàm số đồng biến
c) Tìm m để hàm số đi qua điểm A(2;3)
d) Tìm m để đồ thị cắt trục tung tại điểm có tung độ bằng 9
Bài 8: Cho hàm số y= (2m-3)x+m-5
a) Vẽ đồ thị với m=6
b) Tìm m để đồ thị hàm số tạo với 2 trục tọa độ một tam giác vuông cân
c) Tìm m để đồ thị hàm số tạo với trục hoành một góc 45 độ
Bài 9: Cho hàm số: y= (m-2)x+m+3
a) Tìm m điều kiện của m để hàm số luôn luôn nghịch biến
b) Tìm điều kiện của m để đồ thị cắt trục hoành tại điểm có hoành độ bằng 3
c) Tìm m để đồ thị hàm số tạo với trục tung và trục hoành một tam giác có diện tích bằng 2
Dạng 4: Một số bài tập nâng cao
Bài 1: Giải phương trình: \({x^2} + 4x + 7 = \left( {x + 4} \right)\sqrt {{x^2} + 7} \)
Bài 2: Giải phương trình:
\(\sqrt {2020x – 2019} + 2019x + 2019 = \sqrt {2019x – 2020} \)
Bài 3: Cho hai số thực x,y thay đổi thỏa mãn điều kiện x+y>1 và x>0. Tìm giá trị nhỏ nhất của biểu thức \(M = {y^2} + \frac{{8{x^2} + y}}{{4x}}\)
Bài 4: Cho x,y,z>0 và xy+yz+xz=3xyz. Tính giá trị nhỏ nhất của:
\(A = \frac{{{x^2}}}{{z\left( {{z^2} + {x^2}} \right)}} + \frac{{{y^2}}}{{x\left( {{x^2} + {y^2}} \right)}} + \frac{{{z^2}}}{{y\left( {{y^2} + {z^2}} \right)}}\)
Bài 5: Cho ba số dương x,y,z thay đổi nhưng luôn thỏa mãn điều kiện x+y+z=1. Tìm giá trị lớn nhất của biểu thức: \(P = \frac{x}{{x + 1}} + \frac{y}{{y + 1}} + \frac{z}{{z + 1}}\)
BT tự luận hình học
Bài 1: Cho ( O,R ), lấy điểm A cách O một khoảng bằng 2R. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng OA cắt đường tròn (O) tại I. Đường thẳng qua O và vuông góc với OB cắt AC tại K.
a) Chứng minh: Tam giác OKA cân tại A.
b) Đường thẳng KI cắt AB tại M. Chứng minh: KM là tiếp tuyến của đường tròn (O).
Bài 2: Cho nửa đường tròn tâm O,đường kính AB. Vẽ các tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB. Qua điểm E thuộc nửa đường tròn (E khác A và B) kẽ tiếp tuyến với nửa đường tròn, nó cắt Ax , By theo thứ tự ở C và D.
a) Chứng minh rằng: CD = AC + BD
b) Tính số đo góc \(\widehat {COD}\)?
c) Tính: AC.BD ( Biết OA = 6cm)
Bài 3: Cho tam giác ABC (AB = AC ) kẻ đường cao AH cắt đường tròn tâm O ngoại tiếp tam giác tại D
a) Chứng minh: AD là đường kính;
b) Tính góc ACD
c) Biết AC = AB = 20 cm, BC =24 cm tính bán kính của đường tròn tâm (O).
Bài 4: Cho ( O) và A là điểm nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB; AC với đường tròn (B, C là tiếp điểm )
a) Chứng minh: OA\( \bot \) BC
b) Vẽ đường kính CD chứng minh: BD// AO
c) Tính độ dài các cạnh của tam giác ABC biết OB =2cm; OC = 4 cm?
Bài 5: Cho đường tròn đường kính AB. Qua C thuộc nửa đường tròn kẻ tiếp tuyến d với đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ A, B đến d và H là chân đường vuông góc kẻ từ C đến AB. Chứng minh:
a) CE = CF
b) AC là phân giác của góc BAE
c) CH2 = BF . AE
Bài 6: Cho đường tròn đường kính AB vẽ các tiếp tuyến Ax; By từ M trên đường tròn ( M khác A, B) vẽ tiếp tuyến thứ 3 nó cắt Ax ở C cắt By ở D gọi N là giao điểm của BC Và AO. CMR
a) \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\) b) MN \( \bot \) AB c) góc COD = 90º
Bài 7: Cho đường tròn (O) đường kính AB . Kẻ tiếp tuyến Ax với đường tròn . Điểm C thuộc nửa đường tròn cùng nửa mặt phẳng với Ax với bờ là AB. Phân giác góc ACx cắt đường tròn tại E, cắt BC ở D .Chứng minh :
a)Tam giác ABD cân
b) H là giao điểm của BC và DE . Chứng minh DH vuông góc với AB .
c) BE cắt Ax tại K . Chứng minh tứ giác AKDH là hình thoi
Bài 8: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn, kẻ tiếp tuyến AM, AN ( M, N là các tiếp điểm).
a) Chứng minh OA vuông góc MN
b) Vẽ đường kính NOC; Chứng minh CM song song AO
c) Tính các cạnh của ∆AMN biết OM = 3 cm; OA = 5 cm.
Bài 9: Cho đường nửa tròn (O), đường kính AB. Lấy điểm M trên đường tròn(O), kẻ tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn tại C và D; AM cắt OC tại E, BM cắt OD tại F.
a) Chứng minh \(\widehat {COD} = {90^0}\).
b) Tứ giác MEFO là hình gì?
c) Chứng minh AB là tiếp tuyến của đường tròn đường đường kính CD.
Loigiaihay.com






