Đề cương lý thuyết ôn tập học kỳ I môn toán lớp 12>
Lựa chọn câu để xem lời giải nhanh hơn
PHẦN 1.
ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
1. Sự đồng biến, nghịch biến của hàm số
Điều kiện để hàm số đồng biến, nghịch biến trên khoảng \(\left( {a;b} \right)\)
+) Để hàm số đồng biến trên khoảng \(\left( {a,b} \right)\) thì \(f’\left( x \right) \ge 0,\forall x \in \left( {a,b} \right)\).
+) Để hàm số nghịch biến trên khoảng \(\left( {a,b} \right)\) thì \(f’\left( x \right) \le 0,\forall x \in \left( {a,b} \right).\)
2. Cực trị của hàm số
*) Quy tắc 1: (dựa vào dấu hiệu 1)
+) Tính \(y’\)
+) Tìm các điểm tới hạn của hàm số. (tại đó \(y’ = 0\) hoặc \(y’\) không xác định)
+) Lập bảng xét dấu \(y’\) và dựa vào bảng xét dấu và kết luận.
*) Quy tắc 2: (dựa vào dấu hiệu 2)
+) Tính \(f’\left( x \right),f”\left( x \right)\).
+) Giải phương trình \(f’\left( x \right) = 0\) tìm nghiệm.
+) Thay nghiệm vừa tìm vào \(f”\left( x \right)\) và kiểm tra, từ đó suy kết luận.
3. Giá trị lớn nhất và giá tị nhỏ nhất của hàm số
Quy tắc tìm GTLN – GTNN của hàm số:
*) Quy tắc chung: (Thường dùng cho \(D\) là một khoảng)
– Tính \(f’\left( x \right)\), giải phương trình \(f’\left( x \right) = 0\) tìm nghiệm trên \(D.\)
– Lập BBT cho hàm số trên \(D.\)
– Dựa vào BBT và định nghĩa từ đó suy ra GTLN, GTNN.
*) Quy tắc riêng: (Dùng cho \(\left[ {a;b} \right]\)) . Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left[ {a;b} \right]\)
– Tính \(f’\left( x \right)\), giải phương trình \(f’\left( x \right) = 0\) tìm nghiệm trên \(\left[ {a,b} \right]\).
– Giả sử phương trình có các nghiệm \({x_1},{x_2},… \in \left[ {a,b} \right]\).
– Tính các giá trị \(f\left( a \right),f\left( b \right),f\left( {{x_1}} \right),f\left( {{x_2}} \right),…\).
– So sánh chúng và kết luận.
4. Tiệm cận của đồ thị hàm số
+) Đường thẳng \(x = a\) là TCĐ của đồ thị hàm số \(y = f\left( x \right)\) nếu có một trong các điều kiện sau:
\(\mathop {\lim }\limits_{x \to {a^ + }} y = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to {a^ + }} y = – \infty \) hoặc\(\mathop {\lim }\limits_{x \to {a^ – }} y = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to {a^ – }} y = – \infty \)
+) Đường thẳng \(y = b\) là TCN của đồ thị hàm số \(y = f\left( x \right)\) nếu có một trong các điều kiện sau:
\(\mathop {\lim }\limits_{x \to + \infty } y = b\) hoặc \(\mathop {\lim }\limits_{x \to – \infty } y = b\)
5. Bảng biến thiên và đồ thị hàm số
a) Các dạng đồ thị hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\)
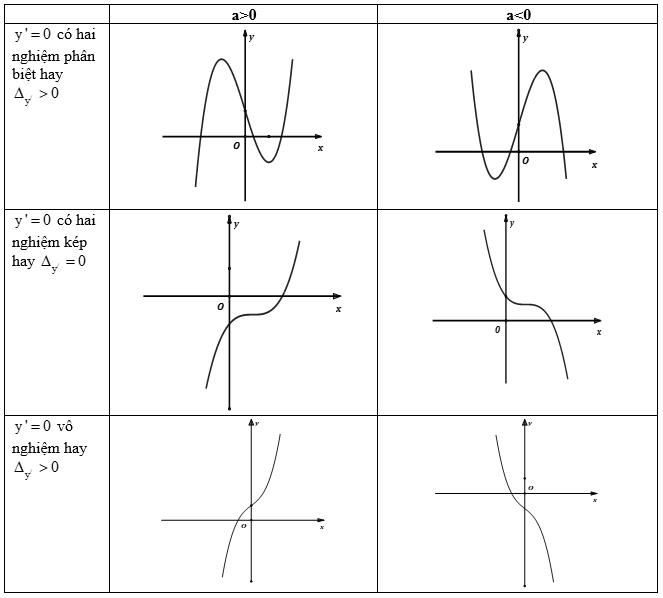
b) Các dạng đồ thị hàm số bậc bốn trùng phương \(y = a{x^4} + b{x^2} + c\)
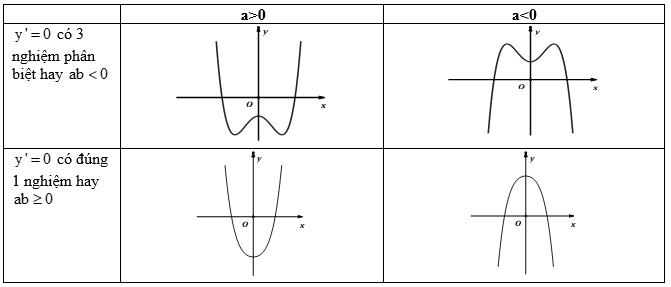
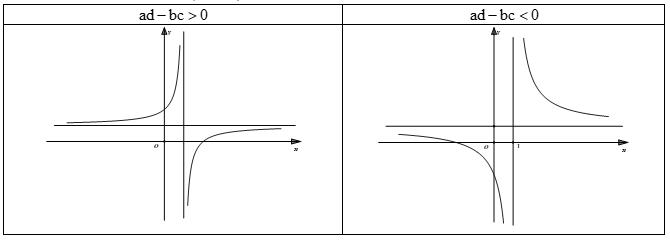
c) Các dạng đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\)
+) Tập xác định: \(D = R\backslash \left\{ { – \dfrac{d}{c}} \right\}\)
+) Đạo hàm: \(y = \dfrac{{ad – bc}}{{{{\left( {cx + d} \right)}^2}}}\)
– Nếu \(ad – bc > 0\) hàm số đồng biến trên từng khoảng xác định. Đồ thị nằm góc phần tư thứ 2 và 4
– Nếu \(ad – bc < 0\) hàm số nghịch biến trên từng khoảng xác định. Đồ thị nằm góc phần tư 1 và 3.
+) Đồ thị hàm số có: TCĐ: \(x = – \dfrac{d}{c}\) và TCN: \(y = \dfrac{a}{c}\)
+) Đồ thị có tâm đối xứng: \(I\left( { – \dfrac{d}{c};\dfrac{a}{c}} \right)\)
Các dạng toán thường gặp
Dạng 1: Tìm các khoảng đơn điệu của hàm số.
Phương pháp:
– Bước 1: Tìm TXĐ của hàm số.
– Bước 2: Tính đạo hàm \(f’\left( x \right)\), tìm các điểm \({x_1},{x_2},…,{x_n}\) mà tại đó đạo hàm bằng \(0\) hoặc không xác định.
– Bước 3: Xét dấu đạo hàm và nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
+ Các khoảng mà \(f’\left( x \right) > 0\) là các khoảng đồng biến của hàm số.
+ Các khoảng mà \(f’\left( x \right) < 0\) là các khoảng nghịch biến của hàm số.
Dạng 2: Tìm giá trị của m để hàm số đơn điệu trên R.
Phương pháp:
– Bước 1: Tính \(f’\left( x \right)\).
– Bước 2: Nêu điều kiện của bài toán:
+ Hàm số \(y = f\left( x \right)\) đồng biến trên \(R \Leftrightarrow y’ = f’\left( x \right) \ge 0,\forall x \in R\) và \(y’ = 0\) tại hữu hạn điểm.
+ Hàm số \(y = f\left( x \right)\) nghịch biến trên \(R \Leftrightarrow y’ = f’\left( x \right) \le 0,\forall x \in R\) và \(y’ = 0\) tại hữu hạn điểm.
– Bước 3: Từ điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất, tam thức bậc hai để tìm \(m\).
Dạng 3: Tìm cực trị của hàm số.
Phương pháp:
Có thể tìm cực trị của hàm số bởi một trong hai quy tắc ở trên.
Chú ý: Đối với các bài toán tìm cực trị của hàm số lượng giác thì dùng quy tắc 2 sẽ thuận tiện hơn, tránh được việc xét dấu đạo hàm.
Dạng 4: Tìm điều kiện của tham số để hàm số có GTLN, GTNN thỏa mãn điều kiện cho trước.
Cho hàm số \(f\left( x \right)\) xác đinh và liên tục trên đoạn \(\left[ {a;b} \right]\).
Phương pháp: (chỉ áp dụng cho một số bài toán dễ dàng tìm được nghiệm của \(y’\))
– Bước 1: Tính \(y’\), giải phương trình \(y’ = 0\) tìm các nghiệm \({x_1},{x_2},…{x_n}\).
– Bước 2: Tính các giá trị \(f\left( a \right),f\left( {{x_1}} \right),…,f\left( {{x_n}} \right),f\left( b \right)\).
– Bước 3: Biện luận theo tham số để tìm GTLN, GTNN của hàm số trên đoạn \(\left[ {a;b} \right]\).
– Bước 4: Thay vào điều kiện bài cho để tìm \(m\).
Dạng 5. Tìm tiệm cận đứng, tiệm cận ngang của đồ thị hàm số
– Bước 1: Tìm các điểm mà tại đó hàm số không xác định.
– Bước 2: Tính các giới hạn\(\mathop {\lim }\limits_{x \to + \infty } y\), \(\mathop {\lim }\limits_{x \to – \infty } y\), \(\mathop {\lim }\limits_{x \to x_0^ + } y\) và \(\mathop {\lim }\limits_{x \to x_0^ – } y\)
– Bước 3: Kết luận:
Nếu xảy ra một trong 4 trường hợp \(\left[ \begin{array}{l}\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty \\\mathop {\lim }\limits_{x \to x_0^ + } y = – \infty \\\mathop {\lim }\limits_{x \to x_0^ – } y = + \infty \\\mathop {\lim }\limits_{x \to x_0^ – } y = – \infty \end{array} \right.\)
thì \(x = {x_0}\) là một tiệm cận đứng của đồ thị hàm số.
Đường thẳng \(y = {y_0}\) được gọi là tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\) nếu nó thỏa mãn một trong 2 điều kiện sau: \(\left[ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\\\mathop {\lim }\limits_{x \to – \infty } y = {y_0}\end{array} \right.\)
Dạng 6: Tìm điều kiện của tham số để đồ thị hàm số phân thức có tiệm cận đứng.
Phương pháp:
– Bước 1: Tìm điều kiện để mẫu thức có nghiệm (nếu cần) và tính các nghiệm \({x_1},{x_2},…,{x_n}\) của mẫu thức.
– Bước 2: Nêu điều kiện để hàm phân thức có tiệm cận đứng:
Hàm số có một (hai, ba,…) tiệm cận đứng nếu mẫu thức có một (hai, ba,…) nghiệm không là nghiệm của tử thức.
– Bước 3: Thay các nghiệm \({x_1},{x_2},…,{x_n}\) lên tử thức và biện luận dựa trên yêu cầu đề bài về số tiệm cận đứng.
Lưu ý: Nếu bài chỉ yêu cầu có tiệm cận đứng thì ta chỉ cần một nghiệm của mẫu không phải nghiệm của tử là đủ.
Dạng 7. Sự tương giao của đồ thị hàm số
a) Tìm giao điểm của hai đồ thị hàm số
Phương pháp:
Cho \(2\) hàm số \(y = f\left( x \right),y = g\left( x \right)\) có đồ thị lần lượt là \(\left( C \right)\) và \(\left( {C’} \right).\)
+) Lập phương trình hoành độ giao điểm của \(\left( C \right)\) và \(\left( {C’} \right):\)\(f\left( x \right) = g\left( x \right)\,\,\,\left( * \right)\)
+) Giải phương trình tìm \(x\) từ đó suy ra \(y\) và tọa độ giao điểm.
+) Số nghiệm của \(\left( * \right)\) là số giao điểm của \(\left( C \right)\) và \(\left( {C’} \right).\)
b) Tương giao của đồ thị hàm số bậc ba
Phương pháp 1: Bảng biến thiên (PP đồ thị)
+) Lập phương trình hoành độ giao điểm dạng \(F\left( {x,m} \right) = 0\) (phương trình ẩn \(x\) tham số \(m\))
+) Cô lập \(m\) đưa phương trình về dạng \(m = f\left( x \right)\)
+) Lập BBT cho hàm số \(y = f\left( x \right)\).
+) Dựa vào giả thiết và BBT từ đó suy ra \(m.\)
*) Dấu hiệu: Sử dụng PP bảng biến thiên khi \(m\) độc lập với \(x.\)
Phương pháp 2: Nhẩm nghiệm – tam thức bậc 2.
+) Lập phương trình hoành độ giao điểm \(F\left( {x,m} \right) = 0\)
+) Nhẩm nghiệm: (Khử tham số). Giả sử \(x = {x_0}\) là \(1\) nghiệm của phương trình.
+) Phân tích: \(F\left( {x,m} \right) = 0 \Leftrightarrow \left( {x – {x_0}} \right).g\left( x \right) = 0 \\\Leftrightarrow \left[ \begin{array}{l}x = {x_0}\\g\left( x \right) = 0\end{array} \right.\) (\(g\left( x \right) = 0\) là phương trình bậc \(2\) ẩn \(x\) tham số \(m\)).
+) Dựa vào yêu cầu bài toán đi xử lý phương trình bậc \(2\) \(g\left( x \right) = 0\).
Dạng 8: Viết phương trình tiếp tuyến của đồ thị
a) Viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm.
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\), viết phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right) \in \left( C \right)\).
Phương pháp:
– Bước 1: Tính \(y’ = f’\left( x \right) \Rightarrow f’\left( {{x_0}} \right)\).
– Bước 2: Viết phương trình tiếp tuyến \(y = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right) + f\left( {{x_0}} \right)\)
– Bước 3: Kết luận.
b) Viết phương trình tiếp tuyến của đồ thị hàm số đi qua một điểm.
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\), viết phương trình tiếp tuyến của \(\left( C \right)\) biết tiếp tuyến đi qua điểm \(M\left( {{x_M};{y_M}} \right)\).
Phương pháp:
– Bước 1: Tính \(y’ = f’\left( x \right)\).
– Bước 2: Viết phương trình tiếp tuyến tại điểm có hoành độ \({x_0}\) của \(\left( C \right)\): \(y = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right) + f\left( {{x_0}} \right)\).
– Bước 3: Thay tọa độ \(\left( {{x_M};{y_M}} \right)\) vào phương trình trên, giải phương trình tìm \({x_0}\).
– Bước 4: Thay mỗi giá trị \({x_0}\) tìm được vào phương trình tiếp tuyến ta được phương trình cần tìm.
c) Viết phương trình tiếp tuyến của đồ thị hàm số cho biết hệ số góc.
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\). Viết phương trình tiếp tuyến của \(\left( C \right)\) biết nó có hệ số góc \(k\).
Phương pháp:
– Bước 1: Tính \(y’ = f’\left( x \right)\).
– Bước 2: Giải phương trình \(f’\left( x \right) = k\) tìm nghiệm \({x_1},{x_2},…\).
– Bước 3: Viết phương trình tiếp tuyến của đồ thị hàm số tại các điểm \(\left( {{x_1};f\left( {{x_1}} \right)} \right),\left( {{x_2};f\left( {{x_2}} \right)} \right),…\)






