Đề cương lý thuyết học kì 1 – Vật lí 11>

Lựa chọn câu để xem lời giải nhanh hơn

Chương 1

CHƯƠNG 1: ĐIỆN TÍCH. ĐIỆN TRƯỜNG

I. Điện tích

1. Điện tích:

– Có hai loại điện tích: điện tích dương và điện tích âm.

– Kí hiệu : q

– Đơn vị: Culông (C)

2. Điện tích nguyên tố

– Có giá trị \(q = 1,{6.10^{ – 19}}\). Hạt electron và hạt proton là hai điện tích nguyên tố.

– Điện tích của hạt (vật) luôn là số nguyên lần điện tích nguyên tố: \(q =  \pm ne\)

3. Vật dẫn điện, điện môi

– Vật (chất) dẫn điện là vật (chất) có chứa nhiều điện tích tự do.

– Vật (chất) cách điện là vật (chất) không chứa hoặc chứa rất ít điện tích tự do.

– Có ba cách nhiễm điện một vật: Cọ xát, tiếp xúc, hưởng ứng.

4. Định luật bảo toàn điện tích

Trong một hệ cô lập về điện (hệ không trao đổi điện tích với các hệ khác) thì tổng đại số các điện tích trong hệ là không đổi.

II. Định luật Culông

Lực tương tác giữa hai điện tích điểm \({q_1},{q_2}\) đặt cách nhau một khoảng r trong môi trường có hằng số điện môi \(\varepsilon \) là \(\overrightarrow {{F_{12}}} ,\overrightarrow {{F_{21}}} \) có:

– Điểm đặt: trên 2 điện tích

– Phương: đường nối hai điện tích

– Chiều:

+ Hướng ra xa nhau nếu \({q_1},{q_2}\) cùng dấu.

+ Hướng vào nhau nếu \({q_1},{q_2}\) trái dấu

– Độ lớn: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}};k = {9.10^9}\left( {\frac{{N.{m^2}}}{{{C^2}}}} \right)\)

III. Cường độ điện trường

1. Khái niệm điện trường

– Điện trường là một dạng vật chất (môi trường) bao quanh điện tích và gắn liền với điện tích. Nó tác dụng lực điện lên các điện tích khác đặt trong nó.

– Đường sức điện trường: Là đường được vẽ trong điện trường sao cho hướng của tiếp tuyến tại bất kì điểm nào trên đường cũng trùng với hướng của vecto cường độ điện trường tại điểm đó.

– Tính chất của đường sức:

+ Qua mỗi điểm trong điện trường ta chỉ có thể vẽ được một và chỉ một đường sức điện trường.

+ Các đường sức điện là các đường cong không kín, nó xuất phát từ các điện tích dương, tận cùng ở các điện tích âm.

– Các đường sức điện không bao giờ cắt nhau.

– Nơi nào có cường độ điện trường lớn hơn thì các đường sức ở đó vẽ mau và ngược lại.

2. Cường độ điện trường

Cường độ điện trường tại một điểm là đại lượng đặc trưng cho tính chất mạnh yếu của điện trường về phương diện tác dụng lực. Nó được xác định bằng thương số của độ lớn lực điện F tác dụng lên một điện tích thử q (dương) đặt tại điểm đó và độ lớn của điện tích q.

\(E = \frac{F}{q}\)

3. \(\overrightarrow {{E_M}} \) tại điểm M do một điện tích điểm gây ra có:

– Gốc tại M

– Phương nằm trên đường thẳng OM,  

– Chiều:

+ Hướng ra xa Q nếu Q > 0

+ Hướng lại gần Q nếu Q < 0

– Độ lớn: \(E = k\frac{{\left| Q \right|}}{{\varepsilon {r^2}}}\)

4. Lực điện trường tác dụng lên điện tích q nằm trong điện trường:

\(\overrightarrow F  = q\overrightarrow E \)

5. Nguyên lý chồng chất: \(\overrightarrow E  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}}  + \overrightarrow {{E_3}}  + … + \overrightarrow {{E_n}} \)

– Nếu \(\left( {\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} } \right) = \alpha \) bất kì thì: \({E^2} = E_1^2 + E_2^2 + 2{{\rm{E}}_1}{E_2}\cos \alpha \)

– Các trường hợp đặc biệt:

+ Nếu \(\overrightarrow {{E_1}}  \uparrow  \uparrow \overrightarrow {{E_2}} \) thì \(E = {E_1} + {E_2}\)

+ Nếu \(\overrightarrow {{E_1}}  \uparrow  \downarrow \overrightarrow {{E_2}} \) thì \(E = \left| {{E_1} – {E_2}} \right|\)

+ Nếu \(\overrightarrow {{E_1}}  \bot \overrightarrow {{E_2}} \) thì \({E^2} = E_1^2 + E_2^2\)

+ Nếu \({E_1} = {E_2}\) thì \(E = 2{{\rm{E}}_1}.\cos \frac{\alpha }{2}\)

IV. Điện trường đều

Điện trường đều là điện trường mà vecto cường độ điện trường tại mọi điểm đều có cùng phương, chiều và độ lớn; đường sức điện là những đường thẳng song song cách đều.

\(E = \frac{U}{d}\) hay U = E.d

V. Công – thế năng – điện thế – hiệu điện thế

1. Công

Công của lực điện tác dụng vào một điện tích không phụ thuộc vào hình dạng đường đi của điện tích mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối của đường đi trong điện trường.

\({A_{MN}} = qEd = qE.s.\cos \alpha  = q.{U_{MN}} \\= q.\left( {{V_M} – {V_N}} \right) = {{\rm{W}}_M} – {{\rm{W}}_N}\)

2. Định lý động năng: (áp dụng cho hạt mang điện chuyển động dọc theo đường sức điện trường)

\({A_{MN}} = q.{U_{MN}} = \frac{1}{2}mv_N^2 – \frac{1}{2}mv_M^2\)

Biểu thức hiệu điện thế: \({U_{MN}} = \frac{{{A_{MN}}}}{q}\)

3. Các định nghĩa

– Điện thế V đặc trưng cho điện trường về phương diện tạo thế năng tại một điểm.

– Thế năng W và hiệu điện thế U đặc trưng cho khả năng sinh công của điện trường.

IV. Tụ điện

1. Công thức định nghĩa:

Điện dung của tụ điện: \(C = \frac{Q}{U}\)

Đơn vị: \(1\mu F = {10^{ – 6}}F;1nF = {10^{ – 9}}F;1pF = {10^{ – 12}}F\)

2. Công thức điện dung của tụ phẳng:

\(C = \frac{{{\varepsilon _0}\varepsilon S}}{d} = \frac{{\varepsilon S}}{{4\pi k{\rm{d}}}}\)

Với S là diện tích phần đối diện giữa hai bản tụ.

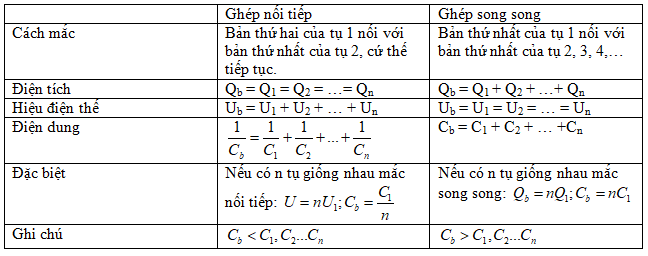
3. Bộ tụ ghép

4. Năng lượng tụ điện:

Tụ điện tích điện thì nó sẽ tích lũy một năng lượng dưới dạng năng lượng điện trường bên trong lớp điện môi.

\({\rm{W}} = \frac{1}{2}QU = \frac{1}{2}C{U^2} = \frac{1}{2}\frac{{{Q^2}}}{C}\)

5. Các trường hợp đặc biệt

– Nối tụ điện vào nguồn: U = const

— Ngắt tụ điện khỏi nguồn: Q = const