Công thức toán học ôn tập thi THPT Quốc Gia

Kỳ thi THPT Quốc Gia đang đến gần đầu tiên các em cần làm là hệ thống lại các công thức Toán thật đầy đủ, chi tiết từ các công thức về lượng giác, công thức tính đạo hàm, nguyên hàm, cấp số cộng, cấp số nhân, đến các công thức tính diện tích hình tam giác, hình chữ nhật, hình tròn,…
Hy vọng với phần tổng hợp Công thức toán ôn thi THPT vào Đại học về nội dung lượng giác, đạo hàm, nguyên hàm, cấp số cộng, cấp số nhân,… ở trên giúp ích cho các em. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi quan trọng này.

I. Công thức về Tam thức bậc hai

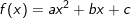
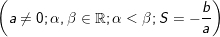
• $small f(x)=ax^{2}+bx+c$ $small left ( a eq 0;alpha ,eta in mathbb{R};alpha < eta ;S=-frac{b}{a} ight )$

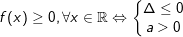
1. small f(x)geq 0,forall xin mathbb{R}Leftrightarrow left{egin{matrix} Delta leq 0 a> 0 end{matrix}
ight.

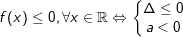
2. small f(x)leq 0,forall xin mathbb{R}Leftrightarrow left{egin{matrix} Delta leq 0 a< 0 end{matrix}
ight.

3. α là nghiệm của f(x) ⇔ f(α)=0.

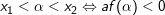
4. $small x_{1}< alpha < x_{2}Leftrightarrow af(alpha )< 0$

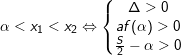
5. $small alpha < x_{1}< x_{2}Leftrightarrowleft{egin{matrix} Delta > 0 af(alpha )> 0 frac{S}{2}-alpha > 0 end{matrix} ight.$

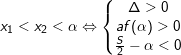
6. $small x_{1}< x_{2}< alpha Leftrightarrowleft{egin{matrix} Delta > 0 af(alpha )> 0 frac{S}{2}-alpha < 0 end{matrix} ight.$

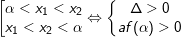
7. $small left [ egin{matrix} alpha < x_{1}< x_{2} x_{1}< x_{2}<alpha end{matrix} Leftrightarrow left{egin{matrix} Delta > 0 af(alpha )> 0 end{matrix} ight.$

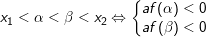
8. $small x_{1}<alpha < eta< x_{2}Leftrightarrowleft{egin{matrix} af(alpha )<0 af(eta )< 0 end{matrix} ight.$

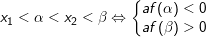
9. $small x_{1}< alpha < x_{2}< eta Leftrightarrow left{egin{matrix} af(alpha )< 0 af(eta )> 0 end{matrix} ight.$

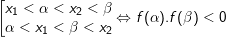
10. $small left [ egin{matrix} x_{1}< alpha < x_{2}< eta alpha <x_{1}< eta < x_{2} end{matrix}Leftrightarrow f(alpha ).f(eta )< 0$

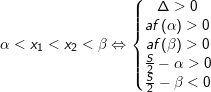
12. $small alpha <x_{1}< x_{2}< eta Leftrightarrowleft{egin{matrix} Delta > 0 af(alpha )> 0 af(eta )> 0 frac{S}{2}-alpha > 0 frac{S}{2}-eta < 0 end{matrix} ight.$

II. Công thức Bất đẳng thức Cauchy (Cô-si).

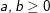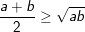1. small a,bgeq 0 thì $small frac{a+b}{2}geq sqrt{ab}$ , dấu “=” xảy ra ⇔ a=b.

2.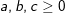 $small dpi{100} fn_cm small a,b,cgeq 0$ thì $small frac{a+b+c}{3}geqsqrt[3]{ abc}$ , dấu “=” xảy ra ⇔ a=b=c.

III. Công thức cấp số cộng

1. Định nghĩa: Dãy số 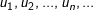$small u_{1}, u_{2},..., u_{n},...$ gọi là cấp số cộng có công sai d nếu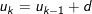 $small u_{k}=u_{k-1}+d$

2. Số hạng thứ n của cấp số cộng là: 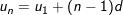$small u_{n}=u_{1}+(n-1)d$

3. Tổng n số hạng đầu tiên của cấp số cộng:

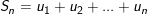
$small dpi{100} fn_cm small S_{n}=u_{1}+u_{2}+...+u_{n}$ $small =frac{n}{2}left ( u_{1}+u_{n} ight )=frac{n}{2}left [ 2u_{1}+(n-1)d ight ]$

IV. Công thức cấp số nhân

1. Định nghĩa: Dãy số 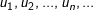$small u_{1}, u_{2},..., u_{n},...$ gọi là cấp số nhân có công bội q nếu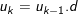 $small u_{k}=u_{k-1}.d$

2. Số hạng thứ n của cấp số nhân: 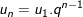$small dpi{100} fn_cm small u_{n}=u_{1}.q^{n-1}$

3. Tổng n số hạng đầu tiên của cấp số nhân:

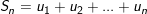
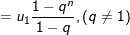
$small S_{n}=u_{1}+u_{2}+...+u_{n}$ $small =u_{1}frac{1-q^{n}}{1-q},(q eq 1)$

• Nếu 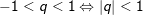small -1<q<1 Leftrightarrow left | q
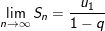
ight |< 1 thì $small lim_{n ightarrow infty }S_{n}=frac{u_{1}}{1-q}$

V. Công thức phương trình, bất phương trình chứa dấu giá trị tuyệt đối

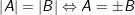
1. small left | A
ight |=left | B
ight |Leftrightarrow A=pm B

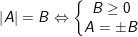
2. small left | A
ight |=BLeftrightarrowleft{egin{matrix} Bgeq 0 A=pm B end{matrix}
ight.

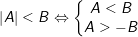
3. small small left | A
ight |< BLeftrightarrowleft{egin{matrix} A< B A> - B end{matrix}
ight.

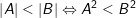
4. $small left | A ight |<left |B ight |Leftrightarrow A^{2}<B^{2}$

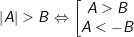
5. small left | A
ight |> BLeftrightarrowleft [ egin{matrix} A> B A< - B end{matrix}

VI. Công thức phương trình và bất phương trình chứa căn thức

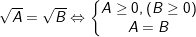
1. small sqrt{A}=sqrt{B}Leftrightarrow left{egin{matrix} Ageq 0 ,(Bgeq 0) A=B end{matrix}
ight.

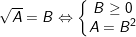
2. $small sqrt{A}=BLeftrightarrow left{egin{matrix} Bgeq 0 A=B^{2} end{matrix} ight.$

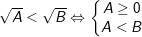
3. small sqrt{A}< sqrt{B}Leftrightarrow left{egin{matrix} Ageq 0 A< B end{matrix}
ight.

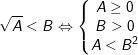
4. $small sqrt{A}< BLeftrightarrow left{egin{matrix} Ageq 0 B> 0 A< B^{2} end{matrix} ight.$

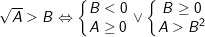
5. $small sqrt{A}> BLeftrightarrow left{egin{matrix} B< 0 Ageq 0 end{matrix} ight.vee left{egin{matrix} Bgeq 0 A> B^{2} end{matrix} ight.$

VII. Công thức phương trình bất phương trình Logarit.

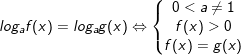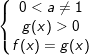
1. $small log_{a}f(x)=log_{a}g(x)Leftrightarrow left{egin{matrix} 0< a eq 1 f(x)> 0 f(x)=g(x) end{matrix} ight.$ hoặc small left{egin{matrix} 0< a
eq 1 g(x)> 0 f(x)=g(x) end{matrix}
ight.

2. $small log_{a}f(x)> log_{a}g(x)Leftrightarrow left{egin{matrix} 0< a eq 1 f(x)> 0g(x)> 0(a-1) [f(x)-g(x)]> 0 end{matrix} ight.$

VIII. Công thức phương trình và bất phương trình mũ

1.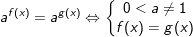 $small a^{f(x)}=a^{g(x)}Leftrightarrow left{egin{matrix} 0< a eq 1 f(x)=g(x) end{matrix} ight.$ hoặc {a=1, f(x),g(x) xác định}.

2. $small a^{f(x)}> a^{g(x)}Leftrightarrow left{egin{matrix} a> 0 (a-1)left [f(x)-g(x ight ]>0end{matrix} ight.$

IX. Công thức tính Lũy thừa.

• Với a,b>0

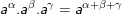
1. $small a^{alpha }.a^{eta }.a^{gamma }=a^{alpha +eta+gamma }$

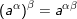
2. $small left (a^{alpha } ight )^{eta }=a^{alpha eta }$

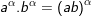
3. $small a^{alpha }.b^{alpha }=left ( ab ight )^{alpha }$

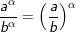
4. $small frac{a^{alpha }}{b^{alpha }}=left ( frac{a}{b} ight )^{alpha }$

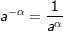
5. $small a^{-alpha }=frac{1}{a^{alpha} }$

6. $small sqrt[n]{a^{k}}=a^{frac{k}{n}}$

7. $small sqrt[m]{sqrt[n]{a^{k}}}=a^{frac{k}{m.n}}$

X. Công thức tính Logarit

• Với 0<N,N1,N2 và 0<a,b≠1 ta có:

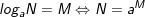
1. $small log_{a}N=MLeftrightarrow N=a^{M}$

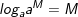
2. $small log_{a}a^{M}=M$

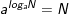
3. $small a^{log_{a}N}=N$

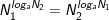
4. $small N_{1}^{log_{a}N_{2}}=N_{2}^{log_{a}N_{1}}$

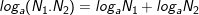
5. $small log_{a}(N_{1}.N_{2})=log_{a}N_{1}+log_{a}N_{2}$

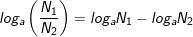
6. $small log_{a}left (frac{N_{1}}{N_{2}} ight )=log_{a}N_{1}-log_{a}N_{2}$

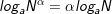
7. $small log_{a}N^{alpha }=alpha log_{a}N$

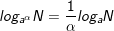
8. $small log_{a^{alpha }}N=frac{1}{alpha }log_{a}N$

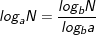
9. $small log_{a}N=frac{log_{b}N}{log_{b}a}$

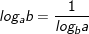
10. $small log_{a}b=frac{1}{log_{b}a}$

XI. Công thức Lượng giác

A. Công thức lượng giác Các hệ thức cơ bản

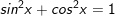
1. $small sin^{2}x+cos^{2}x=1$

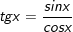
2. $small tgx=frac{sinx}{cosx}$

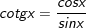
3. $small cotgx=frac{cosx}{sinx}$

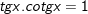
4. small tgx.cotgx=1

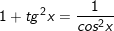
5. $small 1+tg^{2}x=frac{1}{cos^{2}x}$

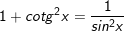
6. $small 1+cotg^{2}x=frac{1}{sin^{2}x}$

B. Công thức lượng giác Các cung liên kết (Đối – Bù – Phụ – Hơn kém π, π/2)

1. cos(-x) = cosx

2. sin(-x) = -sinx

3. tg(-x) = -tgx

4. cotg(-x) = -cotgx

5. sin(π-x)= sinx

6. cos(π-x)= -cosx

7. tg(π-x)= -tgx

8. cotg(π-x)= -cotgx

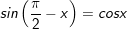
9. $small sinleft (frac{ pi }{2}-x ight )=cosx$

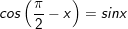
10. $small cosleft (frac{ pi }{2}-x ight )=sinx$

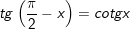
11. $small tgleft (frac{ pi }{2}-x ight )=cotgx$

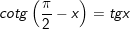
12. $small cotgleft (frac{ pi }{2}-x ight )=tgx$

13. sin(x+π)= -sinx

14. cos(x+π)= -cosx

15. tg(x+π)= tgx

16. cotg(x+π)= cotgx

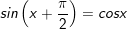
17. $small sinleft (x+frac{pi }{2} ight )=cosx$

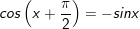
18. $small cosleft (x+frac{pi }{2} ight )=-sinx$

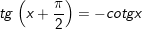
19. $small tgleft (x+frac{pi }{2} ight )=-cotgx$

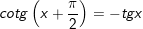
2. $small cotgleft (x+frac{pi }{2} ight )=-tgx$

C. Công thức cộng (các cung lượng giác)

1. sin(x + y) = sinx.cosy + cosx.siny

2. sin(x – y) = sinx.cosy – cosx.siny

3. cos(x + y) = cosx.cosy – sinx.siny

4. cos(x – y) = cosx.cosy + sinx.siny

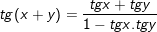
5. $small tg(x+y)=frac{tgx+tgy}{1-tgx.tgy}$

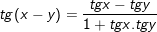
6. $small tg(x-y)=frac{tgx-tgy}{1+tgx.tgy}$

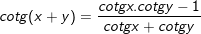
7. $small cotg(x+y)=frac{cotgx.cotgy-1}{cotgx+cotgy}$

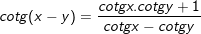
8. $small cotg(x-y)=frac{cotgx.cotgy+1}{cotgx-cotgy}$

D. Công thức nhân đôi (các cung lượng giác).

1. sin2x = 2sinx.cosx

2. cos2x = cos2x – sin2x = 2cos2x – 1 = 1 – 2sin2x

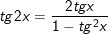
3. $small tg2x=frac{2tgx}{1-tg^{2}x}$

E. Công thức hạ bậc

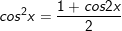
1. $small cos^{2}x=frac{1+cos2x}{2}$

2. $small sin^{2}x=frac{1-cos2x}{2}$

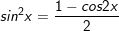
F. Công thức biểu diễn sinx, cosx, tgx theo t=tg(x/2)

• Với 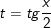$small t=tgfrac{x}{2}$

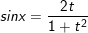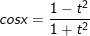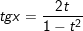
$small sinx=frac{2t}{1+t^{2}}$ ; $small cosx=frac{1-t^{2}}{1+t^{2}}$ ; $small tgx=frac{2t}{1-t^{2}}$

G. Công thức nhân ba (cung lượng giác)

1. sin3x = 3sinx – 4sin3x

2. cos3x = 4cos3x – 3cosx

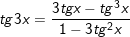
3. $small tg3x=frac{3tgx-tg^{3}x}{1-3tg^{2}x}$

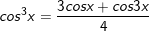
4. $small cos^{3}x=frac{3cosx+cos3x}{4}$

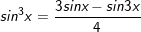
5. $small sin^{3}x=frac{3sinx-sin3x}{4}$

H. Công thức lượng giác biến đổi tích thành tổng

1. $small cosa.cosb = frac{1}{2}left [ cos(a-b)+cos(a+b) ight ]$

2. $small sina.sinb = frac{1}{2}left [ cos(a-b)-cos(a+b) ight ]$

3. $small sina.cosb = frac{1}{2}left [ sin(a-b)+sin(a+b) ight ]$

4. $small cosa.sinb=frac{1}{2}left [ sin(a+b)-sin(a-b) ight ]$

I. Công thức lượng giác biến đổi tổng thành tích

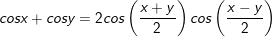
1. $small cosx+cosy=2cosleft ( frac{x+y}{2} ight )cosleft ( frac{x-y}{2} ight )$

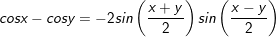
2. $small cosx-cosy=-2sinleft ( frac{x+y}{2} ight )sinleft ( frac{x-y}{2} ight )$

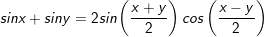
3. $small sinx+siny=2sinleft ( frac{x+y}{2} ight )cosleft ( frac{x-y}{2} ight )$

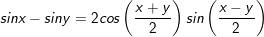
4. $small sinx-siny=2cosleft ( frac{x+y}{2} ight )sinleft ( frac{x-y}{2} ight )$

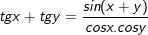
5. $small tgx+tgy=frac{sin(x+y)}{cosx.cosy}$

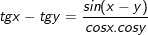
6. $small tgx-tgy=frac{sin(x-y)}{cosx.cosy}$

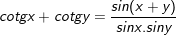
7. $small cotgx+cotgy=frac{sin(x+y)}{sinx.siny}$

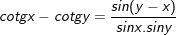
8. $small cotgx-cotgy=frac{sin(y-x)}{sinx.siny}$

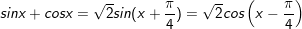
9. $small dpi{100} fn_cm small sinx+cosx=sqrt{2}sin(x+frac{pi }{4})=sqrt{2}cosleft ( x-frac{pi }{4} ight )$

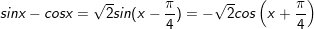
10. $small dpi{100} fn_cm small sinx-cosx=sqrt{2}sin(x-frac{pi }{4})=-sqrt{2}cosleft ( x+frac{pi }{4} ight )$

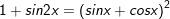
11. $small 1+sin2x=left ( sinx+cosx ight )^{2}$

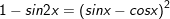
12. $small 1-sin2x=left ( sinx-cosx ight )^{2}$

XII. Công thức phương trình lượng giác

A. Công thức phương trình lượng giác cơ bản

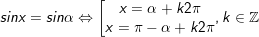
1. small sinx=sinalpha Leftrightarrow left [ egin{matrix} x=alpha +k2pi x=pi -alpha +k2pi end{matrix},kin mathbb{Z}

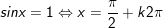
• $small sinx=1Leftrightarrow x=frac{pi }{2}+k2pi$

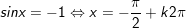
• $small sinx=-1Leftrightarrow x=-frac{pi }{2}+k2pi$

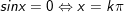
• small sinx=0Leftrightarrow x=kpi

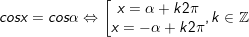
2. small cosx=cosalpha Leftrightarrow left [ egin{matrix} x=alpha +k2pi x=-alpha +k2pi end{matrix},kin mathbb{Z}

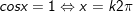
• small cosx=1Leftrightarrow x=k2pi

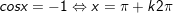
• small cosx=-1Leftrightarrow x=pi +k2pi

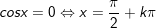
• $small cosx=0Leftrightarrow x=frac{pi }{2}+kpi$

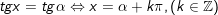
3. small tgx=tgalpha Leftrightarrow x=alpha +kpi ,(kin mathbb{Z})

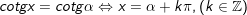
4. small cotgx=cotgalpha Leftrightarrow x=alpha +kpi ,(kin mathbb{Z})

B. Công thức phương trình bậc n theo một hàm số lượng giác.

• Cách giải: Đặt t=sinx (hoặc cosx, tgx, cotgx) ta có phương trình:

antn + an-1tn-1 + … + a0 = 0.

– Nếu t = cosx hoặc t = sinx thì có thêm điều kiện -1≤t≤1.

C. Phương trình bậc nhất theo sinx và cosx

• Phương tình có dạng: asinx + bcosx = c , (a.b≠0)

– Điều kiện phương trình có nghiệm: a2 + b2 ≥ c2.

• Cách giải: Chia 2 vế của phương trình cho 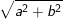$small sqrt{a^{2}+b^{2}}$ và sau đó đưa về phương trình lượng giác cơ bản.

D. Phương trình đẳng cấp bậc 2 đối với sinx và cosx

• Phương trình có dạng: a.sin2x + b.sinx.cosx + c.cos2x = 0

• Cách giải:

° Xét cosx = 0 ⇔ 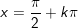$small x=frac{pi }{2}+kpi$ có phải là nghiệm không?

° Xét cosx ≠ 0, chia 2 vế cho cosx và đặt t = tgx.

E. Phương trình lượng giác dạng:

a.(sinx ± cosx) + b.sinx.cosx = c

• Cách giải: Đặt t = sinx ± cosx = 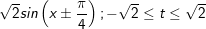$small sqrt{2}sinleft (xpm frac{pi }{4} ight );-sqrt{2}leq tleq sqrt{2}$

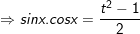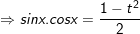$small Rightarrow sinx.cosx=frac{t^{2}-1}{2}$ hoặc $small Rightarrow sinx.cosx=frac{1-t^{2}}{2}$ sau đó giải phương trình bậc 2 theo t.

XIII. Công thức hệ thức lượng trong tam giác.

A. Công thức hàm số cosin:

1. a2 = b2 + c2 – 2bc.cosA

2. b2 = a2 + c2 – 2ac.cosB

3. c2 = a2 + b2 – 2ab.cosC

B. Công thức hàm số sin:

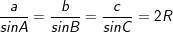
$small frac{a}{sinA}=frac{b}{sinB}=frac{c}{sinC}=2R$

C. Công thức tính độ dài trung tuyến trong tam giác:

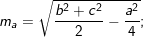
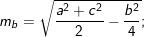
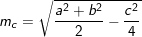
$small m_{a}=sqrt{frac{b^{2}+c^{2}}{2}-frac{a^{2}}{4}};$ $small m_{b}=sqrt{frac{a^{2}+c^{2}}{2}-frac{b^{2}}{4}};$ $small m_{c}=sqrt{frac{a^{2}+b^{2}}{2}-frac{c^{2}}{4}}$

D. Công thức tính diện tích tam giác:

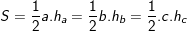
1. $small S=frac{1}{2}a.h_{a}=frac{1}{2}b.h_{b}=frac{1}{2}.c.h_{c}$

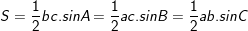
2. $small S=frac{1}{2}bc.sinA=frac{1}{2}ac.sinB=frac{1}{2}ab.sinC$

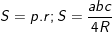
3. $small S=p.r;S=frac{abc}{4R}$

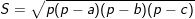
4. small S=sqrt{p(p-a)(p-b)(p-c)}

♦ Lưu ý: trong đó p là nửa chu vi, r bán kính đường tròn nội tiếp tam giác, R bán kính đường tròn ngoại tiếp tam giác.

XIV. Công thức tính Đạo hàm

A. Công thức đạo hàm các hàm cơ bản

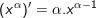
1. $small (x^{alpha })'=alpha .x^{alpha -1}$

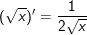
2. $small (sqrt{x})'=frac{1}{2sqrt{x}}$

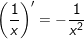
3. $small left ( frac{1}{x} ight )'=-frac{1}{x^{2}}$

4. small (sinx)'=cosx

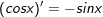
5. small (cosx)'=-sinx

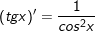
6. $small (tgx)'=frac{1}{cos^{2}x}$

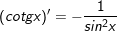
7. $small (cotgx)'=-frac{1}{sin^{2}x}$

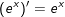
8. $small (e^{x})'=e^{x}$

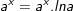
9. $small a^{x}=a^{x}.lna$

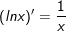
10. $small (lnx)'=frac{1}{x}$

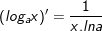
11. $small (log_{a}x)'=frac{1}{x.lna}$

B. Công thức đạo hàm của hàm hợp

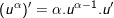
1. $small (u^{alpha })'=alpha .u^{alpha -1}.u'$

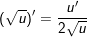
2. $small (sqrt{u})'=frac{u'}{2sqrt{u}}$

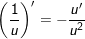
3. $small left ( frac{1}{u} ight )'=-frac{u'}{u^{2}}$

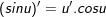
4. small (sinu)'=u'.cosu

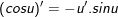
5. small (cosu)'=-u'.sinu

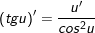
6. $small (tgu)'=frac{u'}{cos^{2}u}$

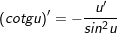
7. $small (cotgu)'=-frac{u'}{sin^{2}u}$

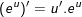
8. $small (e^{u})'=u'.e^{u}$

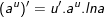
9. $small dpi{100} fn_cm small (a^{u})'=u'.a^{u}.lna$

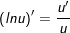
10. $small (lnu)'=frac{u'}{u}$

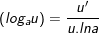
11. $small (log_{a}u)=frac{u'}{u.lna}$

XV. Công thức tính Nguyên hàm

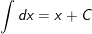
1. small int dx=x+C

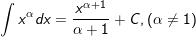
2. $small int x^{alpha }dx=frac{x^{alpha +1}}{alpha +1}+C,(alpha eq 1)$

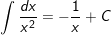
3. $small int frac{dx}{x^{2}}=-frac{1}{x}+C$

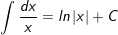
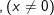
4. $small int frac{dx}{x}=lnleft | x ight |+C$ small ,(x
eq 0)

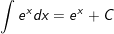
5. $small int e^{x}dx=e^{x}+C$

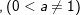
6. $small int a^{x}dx=frac{a^{x}}{lna}+C$ small ,(0< a
eq 1)

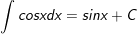
7. small int cosxdx=sinx+C

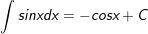
8. small int sinxdx=-cosx+C

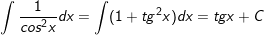
9. $small int frac{1}{cos^{2}x}dx=int (1+tg^{2}x)dx=tgx+C$

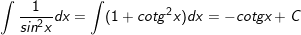
10. $small int frac{1}{sin^{2}x}dx=int (1+cotg^{2}x)dx=-cotgx+C$

XVI. Công thức diện tích hình phẳng – thể tích vật thể tròn xoay:

• Viết phương trình các đường giới hạn hình phẳng.

• Chọn công thức để tính diện tích:

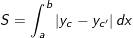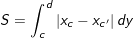
$small S=int_{a}^{b}left | y_{c} -y_{c'} ight |dx$ hoặc $small S=int_{c}^{d}left | x_{c}-x_{c'} ight |dy$

• Chọn công thức để tính thể tích:

– Hình phẳng quay quanh Ox: 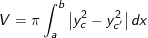$small V=pi int_{a}^{b}left | y_{c}^{2}-y_{c'}^{2} ight |dx$

– Hình phẳng quay quanh Oy: 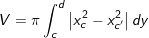$small V=pi int_{c}^{d}left | x_{c}^{2}-x_{c'}^{2} ight |dy$

• Biến x thì cận là x = a; x = b cho trong giả thiết hoặc hoành độ các giao điểm

• Biến y thì cận là y = c; y = d cho trong giả thiết hoặc tung độ các giao điểm

XVII. Công thức cho phương pháp tọa độ trong mặt phẳng:

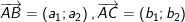
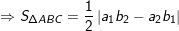
• Với $small overrightarrow{AB}=left ( a_{1};a_{2} ight ),overrightarrow{AC}=left ( b_{1};b_{2} ight )$ $small Rightarrow S_{Delta ABC}=frac{1}{2}left | a_{1} b_{2}-a_{2}b_{1} ight |$

* Các công thức phương trình đường thẳng

a) Phương trình đường thẳng Δ

– Phương trình tổng quát của đường thẳng: Ax + By + C = 0;

(véc-tơ pháp tuyến 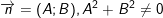$small overrightarrow{n}=(A;B),A^{2}+B^{2} eq 0$ )

– Phương trình tham số của đường thẳng: 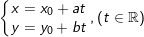$small left{egin{matrix} x=x_{0}+at y=y_{0}+bt end{matrix} ight.,(tin mathbb{R})$

(véc-tơ chỉ phương 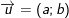small overrightarrow{u}=(a;b) và đi qua điểm M0(x0;y0)).

– Phương trình chính tắc của đường thẳng: 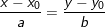$small frac{x-x_{0}}{a}=frac{y-y_{0}}{b}$

– Phương trình đoạn chắn (Δ qua A(a;0); B(0;b)): 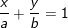$small frac{x}{a}+frac{y}{b}=1$

b) Công thức tính góc φ (00 ≤ φ ≤ 900) giữa hai đường thẳng

• Cho 2 đường thẳng: Ax + By + C = 0 và A’x + B’y + C’ = 0.

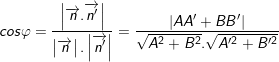
$small cosvarphi =frac{left | overrightarrow{n}. overrightarrow{n'} ight |}{left | overrightarrow{n} ight |.left | overrightarrow{n'} ight |}=frac{left | AA'+BB' ight |}{sqrt{A^{2}+B^{2}}.sqrt{A'^{2}+B'^{2}}}$

c) Khoảng cách từ điểm M0(x0;y0) đến đường thẳng Δ:

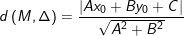
$small dleft ( M,Delta ight )=frac{left | Ax_{0}+By_{0}+C ight |}{sqrt{A^{2}+B^{2}}}$

d) Phương trình đường phân giác của góc tạo bởi 2 đường thẳng

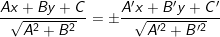
$small frac{ Ax+By+C }{sqrt{A^{2}+B^{2}}}=pm frac{ A'x+B'y+C' }{sqrt{A'^{2}+B'^{2}}}$

e) Hai điểm M1(x1;y1) và M2(x2;y2) nằm cùng một phía so với đường thẳng Δ ⇔ t1.t2>0.

– Hai điểm M1(x1;y1) và M2(x2;y2) nằm khác phía so với đường thẳng Δ ⇔ t1.t2<0.

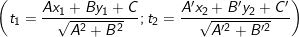
$small left ( t_{1}=small frac{ Ax_{1}+By_{1}+C }{sqrt{A^{2}+B^{2}}}; t_{2}=frac{ A'x_{2}+B'y_{2}+C' }{sqrt{A'^{2}+B'^{2}}} ight )$

XVIII. Các công thức đường tròn

• Phương trình đường tròn:

° Dạng 1: Phương trình đường trong (C) có tâm I(a,;b) và bán kính R

(x – a)2 + (y – b)2 = R2

° Dạng 2: Phương trình có dạng: x2 + y2 – 2ax – 2by + c = 0.

– Với điều kiện a2 + b2 – c> 0 là phương trình đường tròn (C) có tâm I(a;b) và bán kính 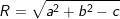$small R=sqrt{a^{2}+b^{2}-c}$

• Phương tích của một điểm M0(x0,y0) đối với một đường tròn:

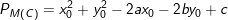
$small P_{M(C)}=x_{0}^{2}+y_{0}^{2}-2ax_{0}-2by_{0}+c$

XIX. Các công thức Elip

• Phương trình chính tắc của Elip (E):

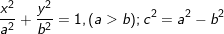
$small frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1,(a> b);c^{2}=a^{2}-b^{2}$

• Tiêu điểm: F1(-c;0), F2(c;0)

• Đỉnh trục lớn: A1(-a;0), A2(a;0)

• Đỉnh trục bé: B1(0;-b), B2(0;b); Tâm sai: 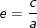$small e=frac{c}{a}$

• Phương trình đường chuẩn: 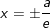$small x=pm frac{a}{e}$

• Phương trình tiếp tuyến của Elip tại M(x0;y0) ∈ (E): 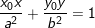$small frac{x_{0}x}{a^{2}}+frac{y_{0}y}{b^{2}}=1$

• Điều kiện tiếp xúc của (E) và (Δ): Ax + By + C = 0 là: A2a2 + B2b2 = C2

XX. Công thức Hypebol

• Phương trình chính tắc của Hypebol: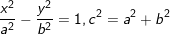 $small frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1,c^{2}=a^{2}+b^{2}$

• Tiêu điểm: F1(-c;0), F2(c;0)

• Đỉnh: A1(-a;0), A2(a;0); Tâm sai: 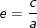$small e=frac{c}{a}$

• Phương trình đường chuẩn: 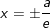$small x=pm frac{a}{e}$

• Phương trình tiệm cận: 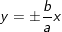$small y=pm frac{b}{a}x$

• Phương trình tiếp tuyến của Hypebol tại M(x0;y0) ∈ (H): 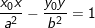$small frac{x_{0}x}{a^{2}}-frac{y_{0}y}{b^{2}}=1$

• Điều kiện tiếp xúc của (H) và (Δ): Ax + By + C = 0 là: A2a2 – B2b2 = C2 (C≠0).

XXI. Công thức Parabol:

• Phương trình chính tắc của Parabol (P): y2 = 2px

• Tiêu điểm: $small Fleft ( frac{p}{2};0 ight )$

• Phương trình đường chuẩn: 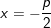$small x=-frac{p}{2}$

• Phương trình tiếp tuyến với (P) tại M(x0;y0)∈(P ): y0y = p(x0 + x)

• Điều kiện tiếp xúc của (P) và (Δ): Ax + By + C = 0 là: 2AC = B2p

XXII. Công thức tính tọa độ trong không gian

1. Công thức tính Tích có hướng của hai véc-tơ:

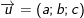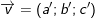
a) Định nghĩa: small overrightarrow{u}=(a;b;c) và small overrightarrow{v}=(a';b';c')

small left [ overrightarrow{u},overrightarrow{v}
ight ]= left ( left | egin{matrix} b &c b' &c' end{matrix}
ight |
ight ); left ( left | egin{matrix} c &a c' &a' end{matrix}
ight |
ight ); left ( left | egin{matrix} a &b a' &b' end{matrix}
ight |
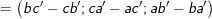
ight ) small =left ( bc'-cb';ca'-ac';ab'-ba'
ight )

b) Các bài tập vận dụng véc-tơ có hướng (ứng dụng của véc-tơ có hướng).

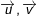• small overrightarrow{u},overrightarrow{v} cùng phương ⇔ small left [overrightarrow{u},overrightarrow{v}
ight ]=overrightarrow{0}

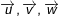• small overrightarrow{u},overrightarrow{v},overrightarrow{w} đồng phẳng ⇔ small left [overrightarrow{u},overrightarrow{v}
ight ].overrightarrow{w}=0

• $small S_{Delta ABC}=frac{1}{2}left | left [ overrightarrow{AB},overrightarrow{AC} ight ] ight |$

• ABCD là tứ diện ⇔ $small left [ overrightarrow{AB},overrightarrow{AC} ight ] .overrightarrow{AD} =m,left (m eq 0 ight ); V_{ABCD}=frac{1}{6}left | m ight |$

2. Công thức mặt phẳng trong không gian

a) Phương trình mặt phẳng (α):

– Phương trình tổng quát của mặt phẳng: Ax + By + Cz + D = 0

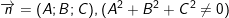
$small overrightarrow{n}=(A;B;C),(A^{2}+B^{2}+C^{2} eq 0)$

– Phương trình đoạn chắn của mặt phẳng: 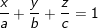$small frac{x}{a}+frac{y}{b}+frac{z}{c}=1$

(Mặt phẳng (α) đi qua 3 điểm A(a;0;0), B(0;b;0) và C(0;0;c)).

b) Góc giữa hai mặt phẳng

(α): Ax + By + Cz + D = 0

(β): A’x + B’y + C’z + D’ = 0

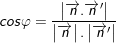
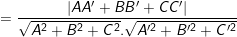
$small cosvarphi =frac{left | overrightarrow{n}.overrightarrow{n}' ight |}{left | overrightarrow{n} ight |.left | overrightarrow{n}' ight |}$ $small =frac{left | AA'+BB'+CC' ight |}{sqrt{A^{2}+B^{2}+C^{2}}.sqrt{A'^{2}+B'^{2}+C'^{2}}}$

c) Khoảng cách từ một điểm M0(x0;y0;z0) đến mặt phẳng (α):

$small dleft [ M_{0},left ( alpha ight ) ight ]=frac{left | Ax_{0}+By_{0}+Cz_{0}+D ight |}{sqrt{A^{2}+B^{2}+C^{2}}}$

3. Công thức phương trình đường thẳng trong không gian

a) Phương trình đường thẳng trong không gian:

• Phương trình chính tắc của đường thẳng: 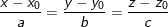$small frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}$

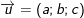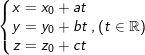
• Phương trình tham số của Δ đi qua M0(x0;y0;z0) và có véc-tơ chỉ phương small overrightarrow{u}=(a;b;c) là: $small left{egin{matrix} x=x_{0}+at y=y_{0}+bt z=z_{0}+ct end{matrix} ight.,(tin mathbb{R})$

• Phương trình tổng quát của đường thẳng: 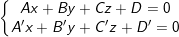small left{egin{matrix} Ax+By+Cz+D=0 A'x+B'y+C'z+D'=0 end{matrix}
ight. với (A:B:C ≠ A’:B’:C’)

b) Góc giữa hai đường thẳng

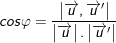
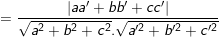
$small cosvarphi =frac{left | overrightarrow{u},overrightarrow{u}' ight |}{left | overrightarrow{u} ight |.left | overrightarrow{u}' ight |}$ $small =frac{left | aa'+bb'+cc' ight |}{sqrt{a^{2}+b^{2}+c^{2}}.sqrt{a'^{2}+b'^{2}+c'^{2}}}$

c) Khoảng cách từ điểm A đến đường thẳng Δ (Δ có VTCP 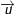và qua M)

$small d left (A,Delta ight )=frac{left | left [ overrightarrow{u} ,overrightarrow{MA} ight ] ight |}{left | overrightarrow{u} ight |}$

d) Khoảng cách giữa hai đường thẳng chéo nhau

– Δ có VTCP 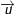small overrightarrow{u} và qua M, Δ’ có VTCP 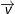small overrightarrow{v} và qua M’

$small d left (Delta,Delta ' ight )=frac{left | left [ overrightarrow{u} ,overrightarrow{v} ight ].overrightarrow{MM'} ight |}{left |left [ overrightarrow{u}, overrightarrow{v} ight ] ight |}$

e) Góc giữa đường thẳng Δ và mặt phẳng (α):

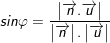
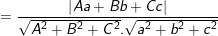
$small sinvarphi =frac{left | overrightarrow{n} .overrightarrow{u} ight |}{left | overrightarrow{n} ight |.left | overrightarrow{u} ight |}$ $small =frac{left | Aa+Bb+Cc ight |}{sqrt{A^{2}+B^{2}+C^{2}}.sqrt{a^{2}+b^{2}+c^{2}}}$

4. Công thức Phương trình mặt cầu

a) Phương trình mặt cầu:

• Dạng 1: Phương trình mặt cầu (S) có tâm I(a;b;c) và bán kính R:

(x – a)2 + (y – b)2 + (y – c)2 = R2

• Dạng 2: Phương trình mặt cầu (S) dạng:

x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0

– Với điều kiện a2 + b2 + c2 – d > 0 là phương trình mặt cầu có tâm I(a;b;c) và bán kính 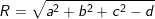$small R=sqrt{a^{2}+b^{2}+c^{2}-d}$ .

b) Sự tương giao giữa mặt cầu và mặt phẳng:

• small dleft [ I,(alpha )
ight ]< R ⇔ (α) giao (S) theo đường tròn (C)

– Phương trình (C): 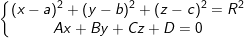$small left{egin{matrix} (x-a)^{2}+(y-b)^{2}+(z-c)^{2}=R^{2} Ax+By+Cz+D=0 end{matrix} ight.$

– Tâm H của (C) là hình chiếu của tâm I(a;b;c) lên mặt phẳng (α)

– Bán kính của (C): 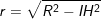$small r=sqrt{R^{2}-IH^{2}}$

• small dleft [ I,(alpha )
ight ]= R ⇔ (α) tiếp xúc với (S)

• small dleft [ I,(alpha )
ight ]> R ⇔ (α) ∩ (S) = ∅

XXIII. Công thức Chỉnh hợp, Tổ hợp, Giai thừa và nhị thức Newton

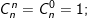
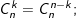
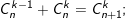
• Tính chất tổ hợp: $small C_{n}^{n}=C_{n}^{0}=1;$ $small C_{n}^{k}=C_{n}^{n-k};$ $small C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k};$

• Công thức tổ hợp: 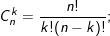$small C_{n}^{k}=frac{n!}{k!(n-k)!};$

• Công thức chỉnh hợp: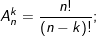 $small A_{n}^{k}=frac{n!}{(n-k)!};$

• Công thức tính giai thừa: 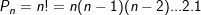$small P_{n}=n!=n(n-1)(n-2)...2.1$

• Nhị thức Newton:

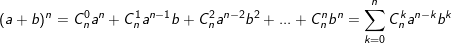
° $small (a+b)^{n}=C_{n}^{0}a^{n}+C_{n}^{1}a^{n-1}b+C_{n}^{2}a^{n-2}b^{2}+...+C_{n}^{n}b^{n}=sum_{k=0}^{n}C_{n}^{k}a^{n-k}b^{k}$

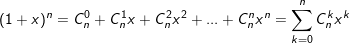
° $small (1+x)^{n}=C_{n}^{0}+C_{n}^{1}x+C_{n}^{2}x^{2}+...+C_{n}^{n}x^{n}=sum_{k=0}^{n}C_{n}^{k}x^{k}$

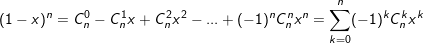
° $small (1-x)^{n}=C_{n}^{0}-C_{n}^{1}x+C_{n}^{2}x^{2}-...+(-1)^{n}C_{n}^{n}x^{n}=sum_{k=0}^{n}(-1)^{k}C_{n}^{k}x^{k}$

Trên đây là những chia sẻ mà Gia Sư Tri Thức muốn gửi đến bạn nếu như bạn đang gặp khó khăn trong học môn Toán 12. Hãy thử áp dụng và bạn sẽ thấy rõ hiệu quả đấy! Nếu bạn đã thử và không thấy cải thiện thành tích và khả năng cảm văn của mình, hãy thử tìm một gia sư dạy kèm toán 12 tại nhà nhé! Trung tâm Gia Sư Tri Thức sẽ giúp bạn.

Với đội ngũ giáo viên dạy toán 12 giỏi của những trường uy tín và sinh viên có trình độ sư phạm, chuyên môn tốt, chắc chắn hiệu quả học tập của bạn sẽ được cải thiện rõ rệt trong thời gian ngắn đến nỗi bạn sẽ không thể tin được!

Hãy liên hệ ngay với Gia Sư Tri Thức để cải thiện kết quả học tập môn Toán của bạn nhé!

TRUNG TÂM GIA SƯ TRÍ THỨC

Nhận dạy kèm tại nhà tất các quận huyện TP.HCM

Hotline: 0776 480 480

Webstie: www.giasutrithuc.net

Fanpage: Gia Sư Tri Thức

Công thức toán học ôn tập thi THPT Quốc Gia – Gia Sư Tri Thức Việt Nam

Công thức toán học ôn tập thi THPT Quốc Gia