Bảng các công thức lượng giác lớp 10, 11, 12 đầy đủ nhất
Công thức lượng giác là một trong những công thức được ứng dụng khá rộng rãi trong toán học đặc biệt là trong các chương trình của Trung Học Phổ Thông lớp 10 , 11 và lớp 12 . Hầu hết các công thứ lượng giác đều có mặt trong các đề thi toán học như cuối năm, thi tốt nghiệp và cả trong đề thi đại học .
Để mà học thuộc các công thức lượng giác thường chúng ta sẽ gặp rất nhiều khó khăn . Chính vì thế để mà học thuộc được toàn bộ công thức của hàm lượng giác thì chúng ta cần mất nhiều thời gian và công sức . Chính vì thế để giúp các bạn học sinh THPT có thể ôn lại được các hàm lượng giác thì Legoland xin được tổng hợp các công thức lượng giác từ lớp 10 , lớp 11 đến lớp 12 nhé .
Nội Dung Chính
Lượng giác là gì?
Lượng giác trong tiếng anh được dịch là Trigonometry (từ tiếng Hy Lạp trigōnon nghĩa là “tam giác” + metron “đo lường” ). Lượng giác chính là một nhánh trong toán học dùng để tìm hiểu về hình tam giác và sự liên hệ giữa cạnh của hình tam giác và góc độ của nó. Lượng giác chỉ ra hàm số lượng giác và nó diễn tả các mối liên kết và có thể áp dụng được để học những hiện tượng có chu kỳ, như sóng âm.
Tham khảo thêm :
Các ứng dụng của lượng giác
Trong toán học thì lượng giác được ứng dụng khá rộng rãi và nó được sử dụng để :
- Giúp chúng ta dễ dàng đo chiều cao và khoảng cách của vật bất kỳ
- Hỗ trợ đo lường trong kiến trúc và kỹ thuật
- Lý thuyết lượng giác trong âm nhạc và sản xuất
- Hỗ trợ hệ thống định vị GPS để xác định vị trí
Tổng hợp bảng các công thức lượng giác lớp 10, 11, 12
Trong công thức lượng giác này thì chúng tôi sẽ tổng hợp lại các kiến thức về lượng giác của các chương trình học THPT từ lớp 10 , lớp 11 đến lớp 12 giúp các bạn có thể hệ thống lại được các công thức để giúp dễ học và dễ hiệu hơn nhé .
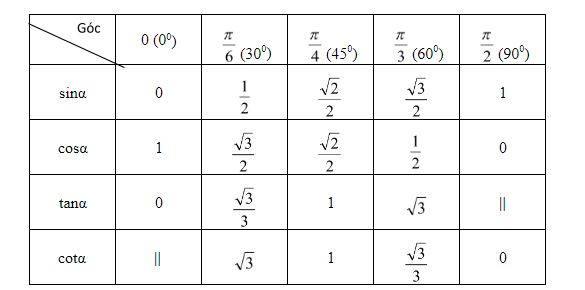
Bảng giá trị lượng giác của cung và góc đặc biệt
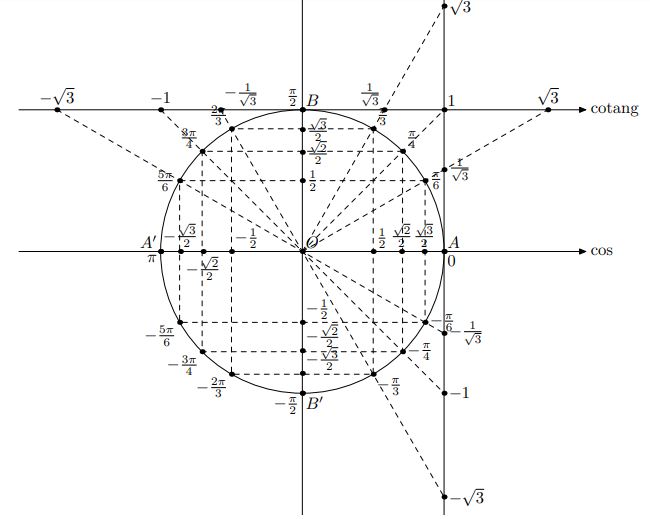
Bảng tính như sau :
Các cung liên quan đặc biệt
Đây là công thức lượng giác đầy đủ về các cung liên quan đặc biệt với nhau theo đúng sách giáo khoa .
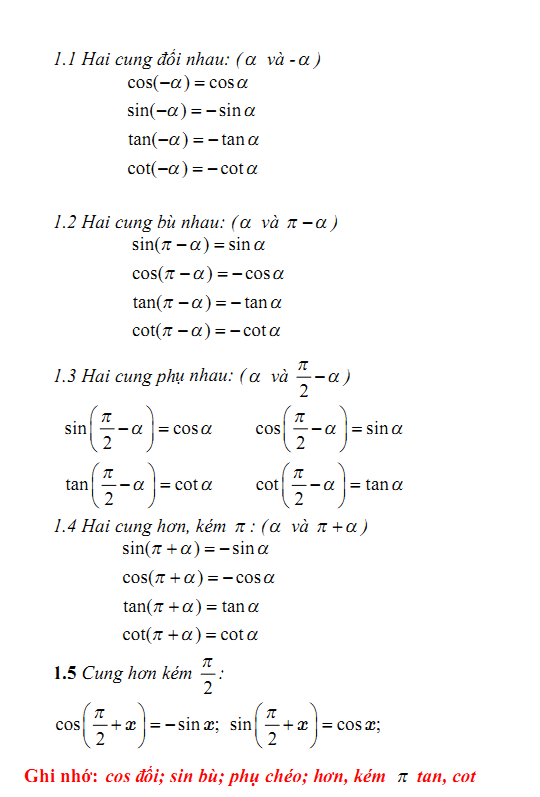
Các công thức lượng giác cơ bản
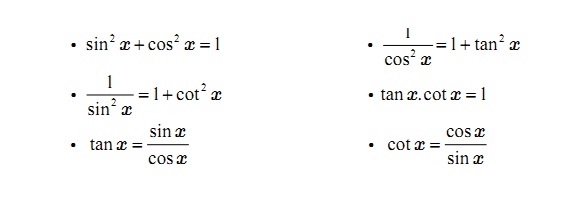
Công thức cộng
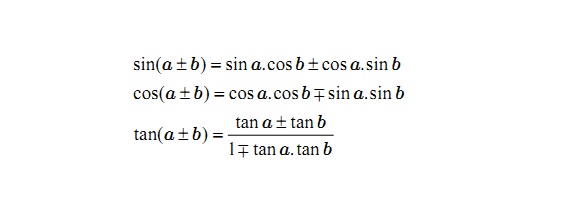
Công thức nhân đôi và nhân 3
Bảng công thức nhân đôi và nhân 3 trong công thức lượng giác đầy đủ trong hàm lượng giác được Legoland liệt kê ra như sau :
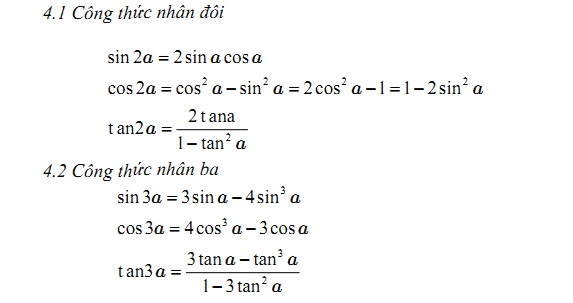
Công thức hạ bậc
Với công thức lượng giác hạ bậc này chúng ta có thể áp dụng để giải các bài toán về các góc lượng giác khác nhau .
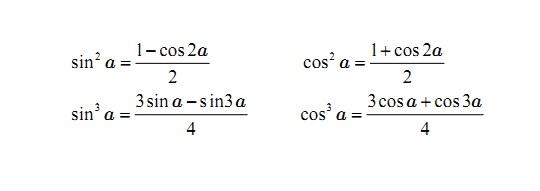
Công thức biến đổi tổng thành tích
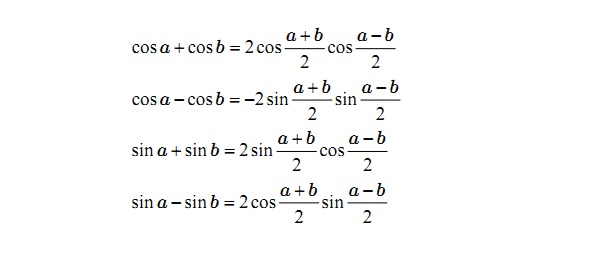
Công thức biến đổi tích thành tổng
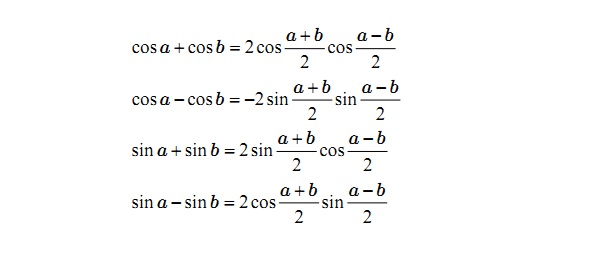
Công thức nghiệm của phương trình lượng giác cơ bản
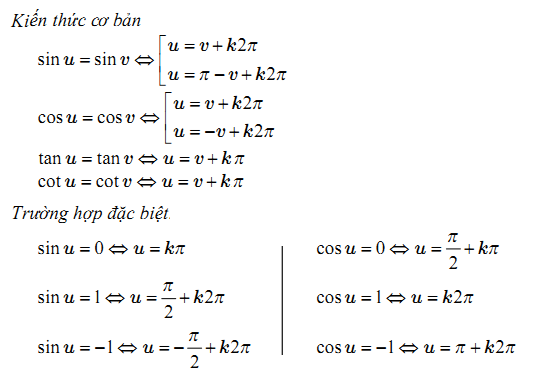
Một số công thức lượng giác khác được dùng nhiều trong tam giác

Hướng dẫn mẹo học thuộc bảng công thức lượng giác nhanh là nhớ lâu
Để giúp mọi người có thể ghi nhớ công thức lượng giác lâu hơn và dễ dàng hơn thì Legoland xin tổng hợp lại cho mọi người những mẹo học theo các câu vì hay các từ đồng âm để có thể nhớ lâu nhất nhé .
Mẹo học thuộc bảng lượng giác cộng trừ
Cos + cos = 2 cos cos
cos trừ cos = trừ 2 sin sin
Sin + sin = 2 sin cos
sin trừ sin = 2 cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin “coi chừng” (dấu trừ).
Tang tổng thì lấy tổng tang
Chia một trừ với tích tang, dễ òm.
Mẹo học bảng giá trị lượng giác của cung đặc biệt
Cos đối, sin bù, phụ chéo, khác pi tan
Cosin của 2 góc đối bằng nhau; sin của 2 góc bù nhau thì bằng nhau; phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia; tan của 2 góc hơn kém pi thì bằng nhau.
Mẹo học thuộc công thức gấp 2
+Sin gấp đôi = 2 sin cos
+Cos gấp đôi = bình cos trừ bình sin
= trừ 1 + 2 lần bình cos
= + 1 trừ 2 lần bình sin
+Tang gấp đôi
Tang đôi ta lấy đôi tang (2 tang)
Chia 1 trừ lại bình tang, ra liền.
Mẹo học hệ thức lượng trong tam giác vuông
Sao Đi Học (Sin = Đối / Huyền)
Cứ Khóc Hoài ( Cos = Kề / Huyền)
Thôi Đừng Khóc ( Tan = Đối / Kề)
Có Kẹo Đây ( Cotan = Kề/ Đối)
Sin : đi học (cạnh đối – cạnh huyền)
Cos: không hư (cạnh đối – cạnh huyền)
Tang: đoàn kết (cạnh đối – cạnh kề)
Cotang: kết đoàn (cạnh kề – cạnh đối)
Tìm sin lấy đối chia huyền
Cosin lấy cạnh kề, huyền chia nhau
Còn tang ta hãy tính sau
Đối trên, kề dưới chia nhau ra liền
Cotang cũng dễ ăn tiền
Kề trên, đối dưới chia liền là ra
Sin bù, cos đối, hơn kém pi tang, phụ chéo.
+Sin bù :Sin(180-a)=sina
+Cos đối :Cos(-a)=cosa
+Hơn kém pi tang :
Tg(a+180)=tga
Cotg(a+180)=cotga
+Phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tg góc này = cotg góc kia.
Công thức tổng quát hơn về việc hơn kém pi như sau:
Hơn kém bội 2 pi sin, cos
Tang, cotang hơn kém bội pi.
Sin(a+k.2.180)=sina ; Cos(a+k.2.180)=cosa
Tg(a+k180)=tga ; Cotg(a+k180)=cotga
*sin bình + cos bình = 1
*Sin bình = tg bình trên tg bình + 1.
*cos bình = 1 trên 1 + tg bình.
*Một trên cos bình = 1 + tg bình.
*Một trên sin bình = 1 + cotg bình.
Câu vè hàm lượng giác
Bắt được quả tang
Sin nằm trên cos
Côtang cãi lại
Cos nằm trên sin!
Mẹo học công thức lượng giác nhân 3
Nhân ba một góc bất kỳ,
sin thì ba bốn, cos thì bốn ba,
dấu trừ đặt giữa 2 ta, lập phương chỗ bốn,
… thế là ok.
Mẹo nhớ công thức: tan(a+b)=(tan+tanb)/1-tana.tanb
tan một tổng 2 tầng cao rộng
trên thượng tầng tan + tan tan
dưới hạ tầng số 1 ngang tàng
dám trừ một tích tan tan oai hùng
Tổng kết :
Với các công thức lượng giác ở trên hi vọng mọi người có thể áp dụng để giải các phương trình lượng giác , các góc và các bài tập liên quan đến công thức lượng giác tốt nhất và nhanh nhất nhé .






